Zyklische Symmetrie findet Anwendung bei der linearen/nichtlinearen Analyse von Strukturen, die sich in n gleiche Teilstrukturen beim Umlauf um eine bestimmte Rotationsachse aufteilen lassen. Hierfür reicht es aus, die Lösung für eine Teilstruktur (sog. Sektor) zu ermitteln.
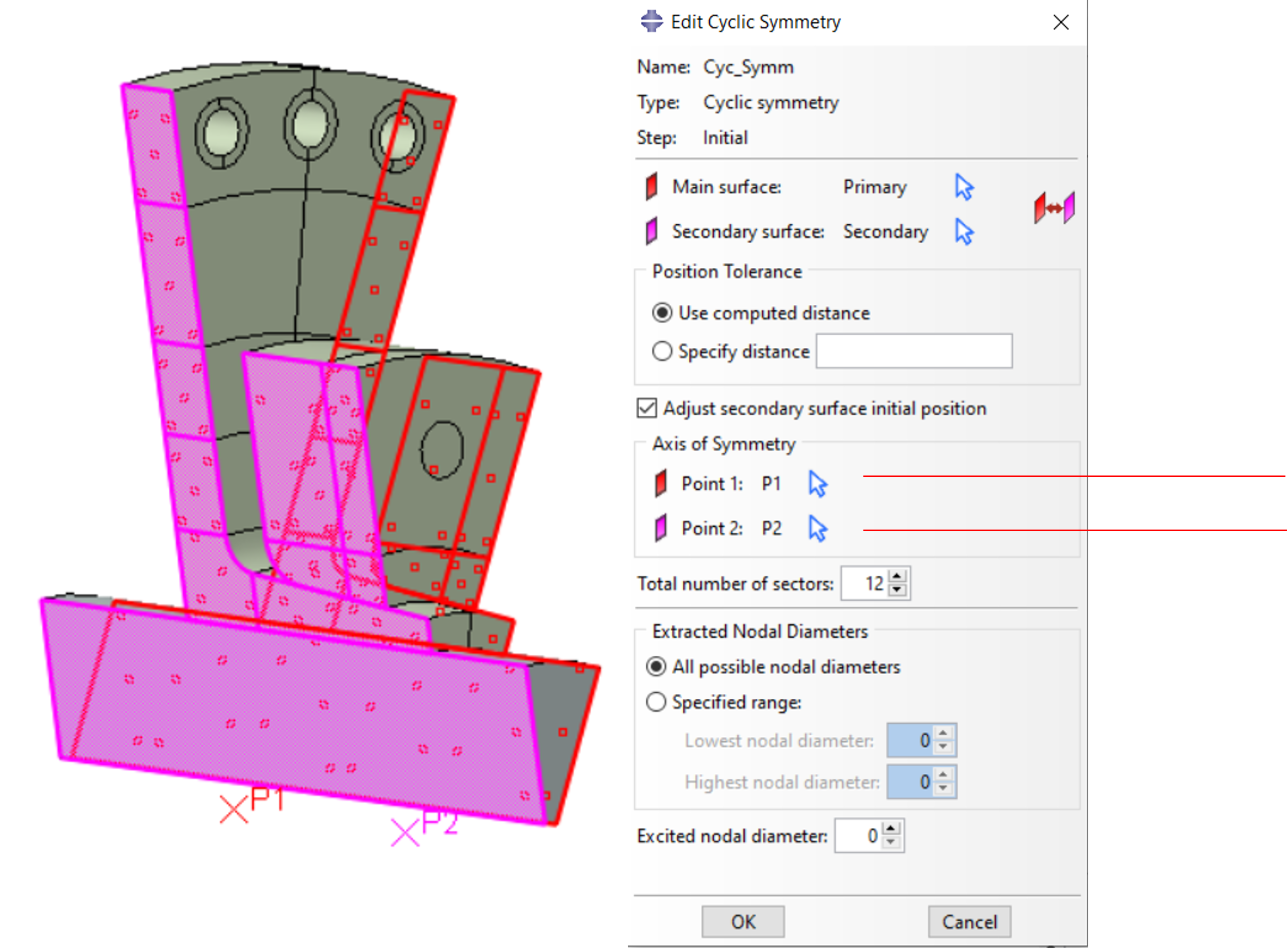
Die Vorgehensweise ist einfach: Aus der Gesamtstruktur wird ein zyklischer Sektor herausgeschnitten. Die Zyklische Symmetrie wird an den Schnittflächen an der Primary und der Secondary Surface über eine Interaktion im INITIAL STEP definiert. Anstatt einer Surface kann auch eine Node Region/Geometry verwendet werden.
Es ist unerheblich, ob die Vernetzungen an der Primary und Secondary Surface identisch sind, es muss aber darauf geachtet werden, dass die feinere Vernetzung immer der Secondary Surface zugewiesen wird.
Hinsichtlich der Lasten gibt es Einschränkungen, welche im ersten Beispiel näher erläutert werden.
Darüber hinaus besteht die Möglichkeit, den erhaltenen Spannungs- und Verformungszustand auf ein 360° Gesamtmodell zu übertragen, um dann nicht-zyklisch symmetrische äußere Lasten aufzubringen, wie z.B. Biegung (ist Inhalt eines separaten Beitrages, s. auch *SYMMETRIC MODEL GENERATION, *SYMMETRIC RESULTS TRANSFER).
Die folgenden beiden Beispiele zeigen auf, wie die zyklische Symmetrie angewendet wird und welche Vorteile diese hat. Die Beispiele wurden mit Abaqus/CAE erstellt. Gerne stellen wir Ihnen die CAE-Datei zur Verfügung.
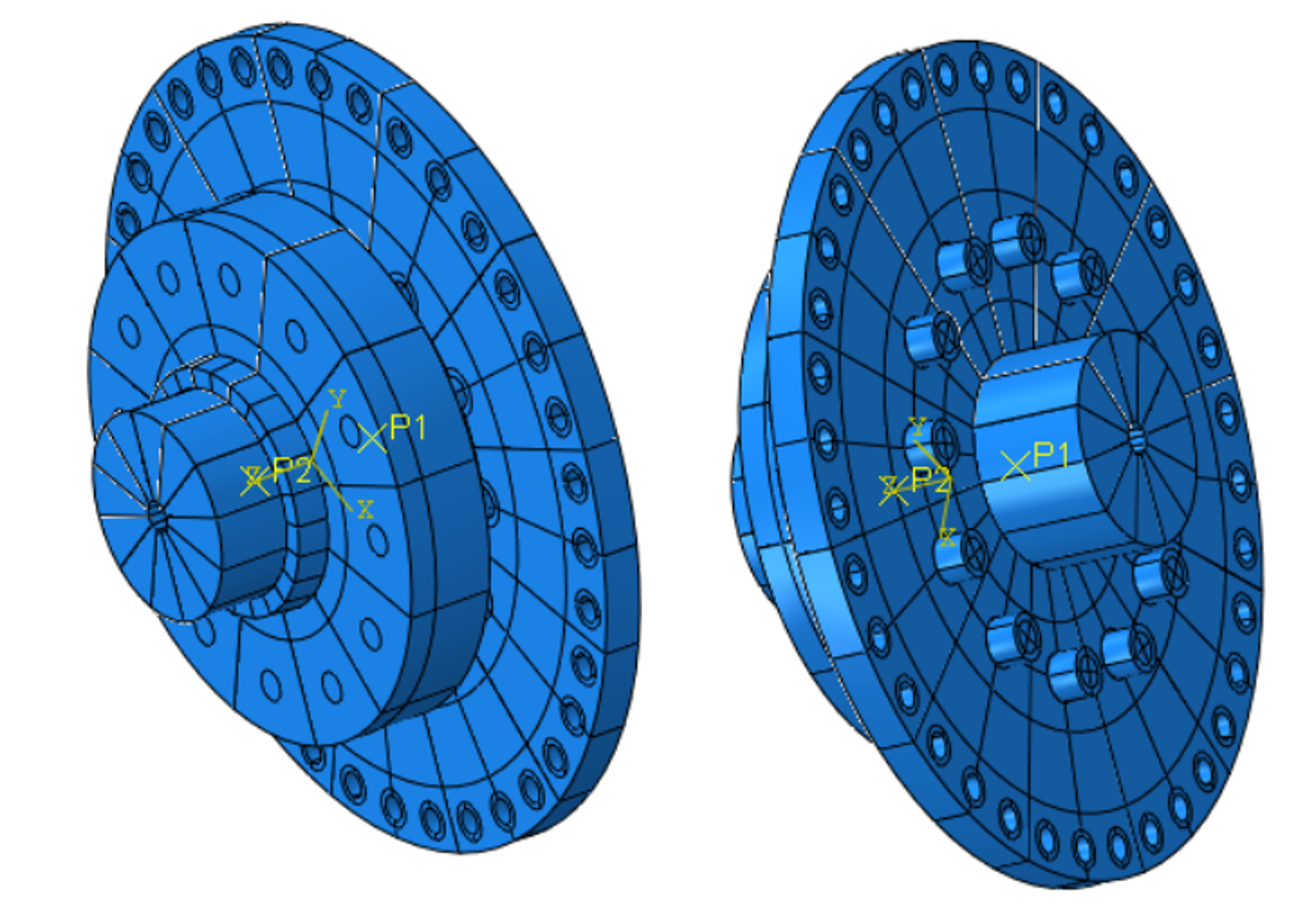
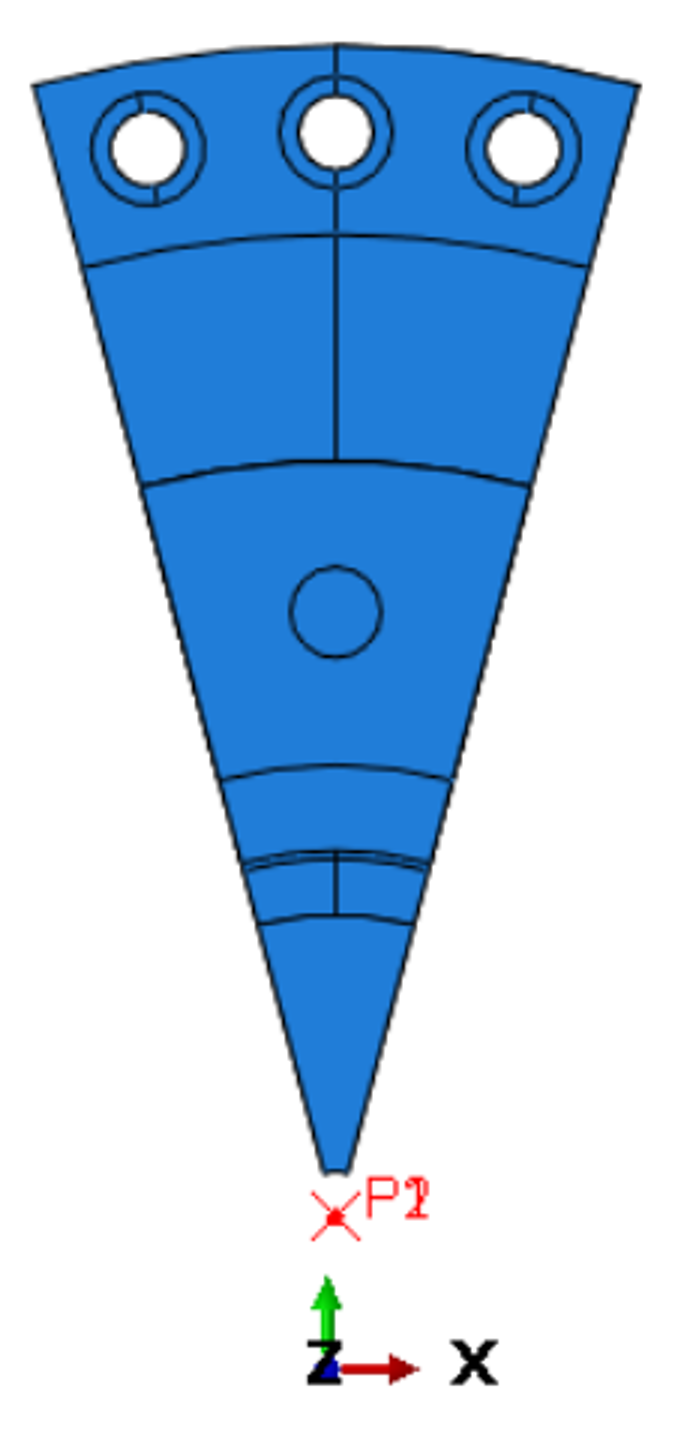
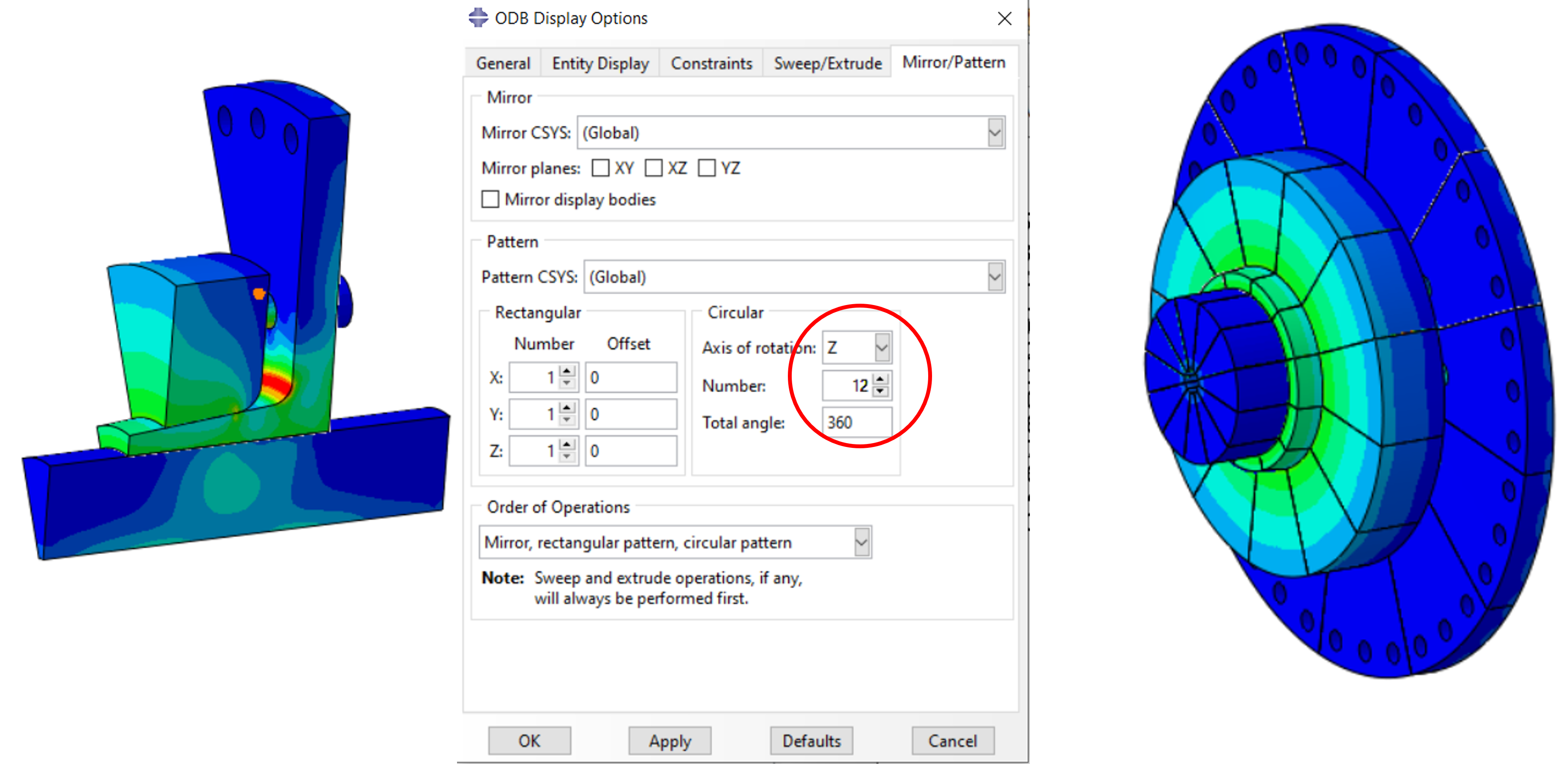
Aus einem Vollmodell einer mit einem Außenteil zu verspannenden Welle ergibt sich, daß ein 30° Ausschnitt zyklisch symmetrisch ist. Er ergeben sich 12 zyklische symmetrische Teile, Für ein Teilmodell und ein Vollmodel wird die Berechnung aufgebaut.
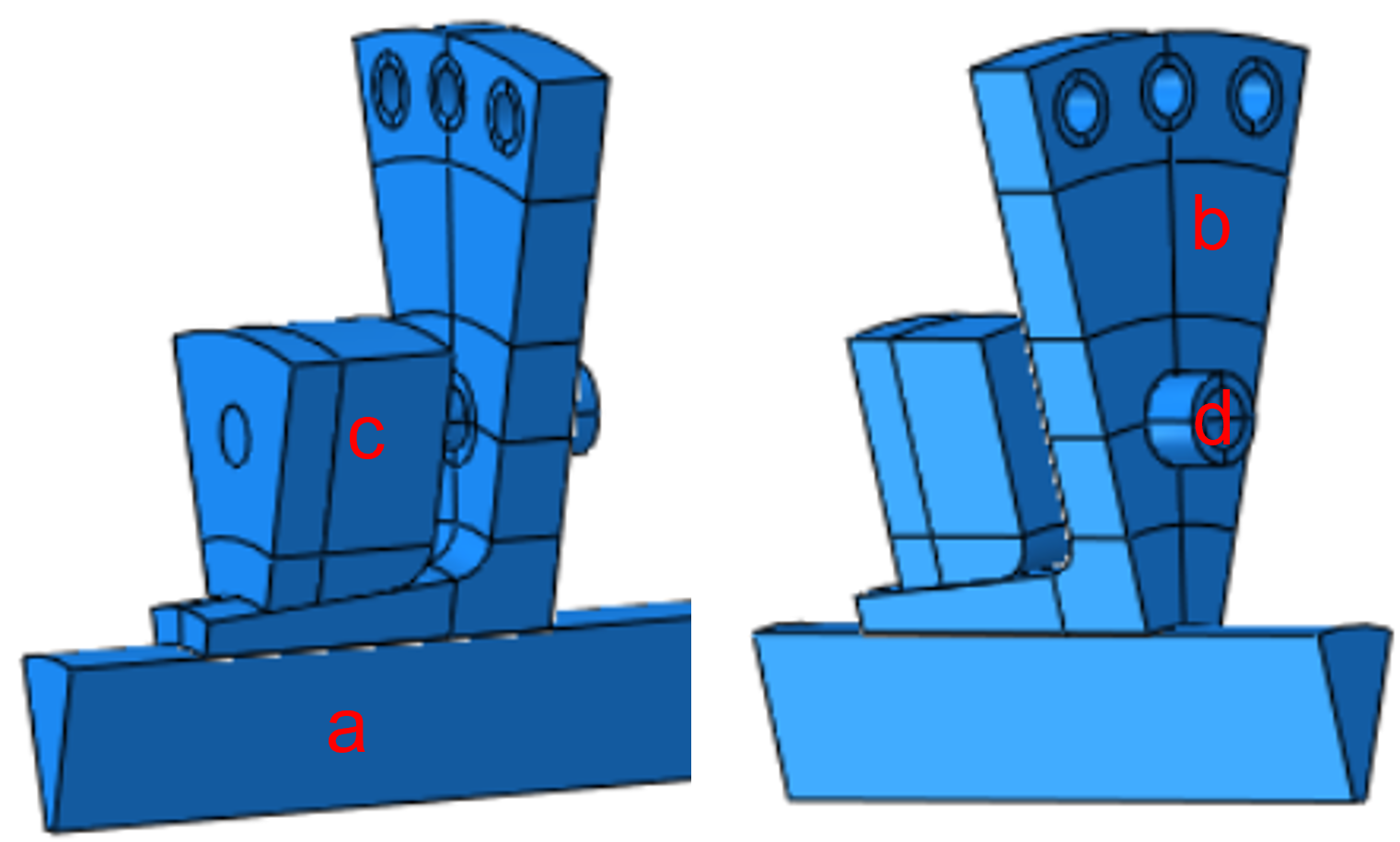
Die Welle (a) wird innen über Knoten-Kopplung vom Typ Kinematic an einen Referenzpunkt auf der Rotationsachse gekoppelt. Dieser Referenzpunkt ist über eine Randbedingung fixiert.
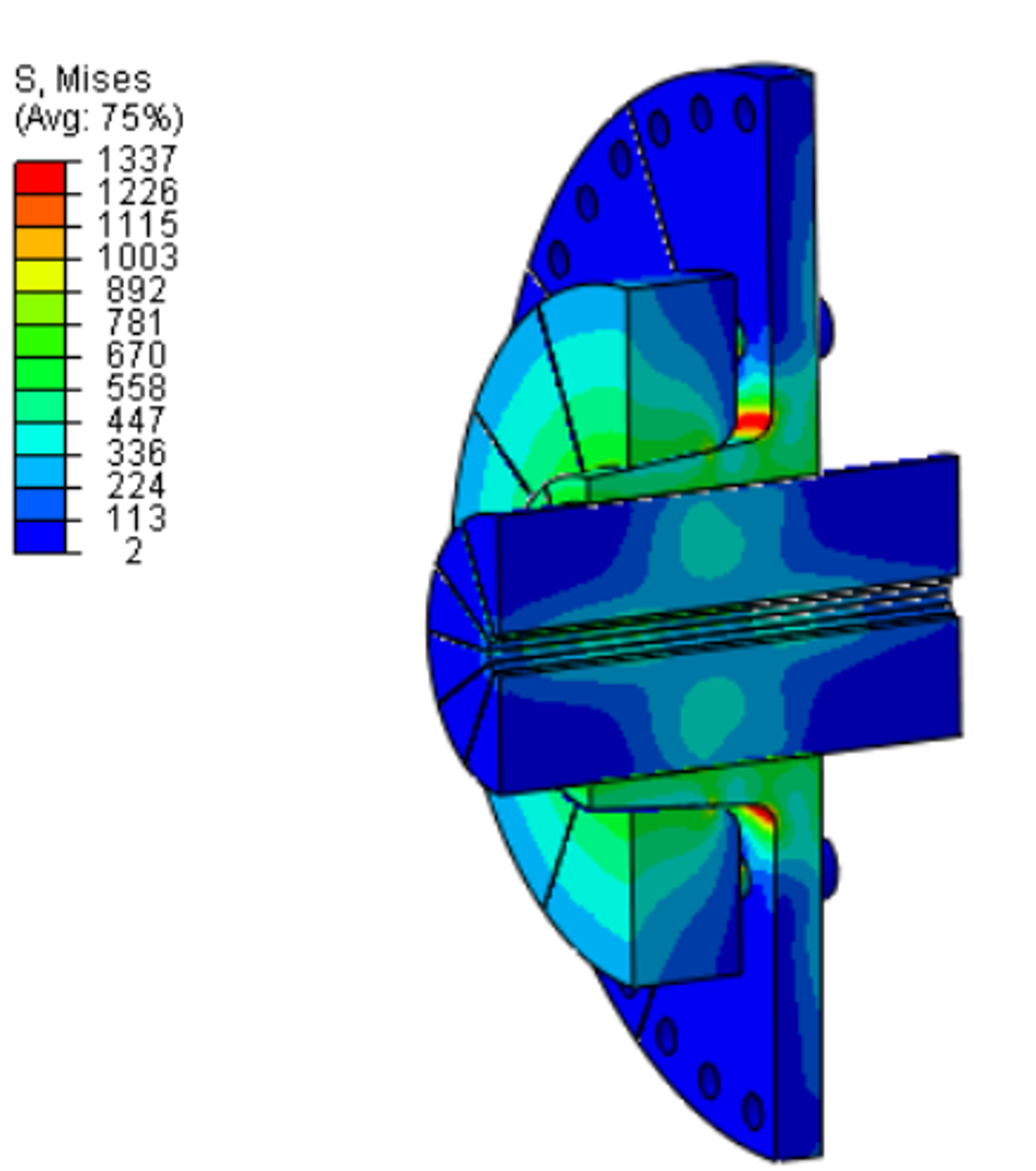
Durch das Verspannen des Innenteils (b) mit dem Außenteil (c) mit einer Schraubenkraft und dem konischen Verlauf des Außenteils im Bereich der Welle kommt es zu einem Verpressen von Innenteil, Außenteil und Welle. Als Step wird ein Static, General mit nicht linearer Geometrie definiert.
Vollmodell
30°-Segment
Definition der Symmetrieachse
Diese Punkte müssen zuvor als Reference Points definiert werden.
Für den Fall, dass sie nicht Teil einer Kopplung sind, erscheinen sie in der DAT-Datei mit einer Warnung, die ignoriert werden kann (unused node).
Während praktisch alle Lasten (Fliehkraft, Temperatur…) auf den Sektor aufgebracht werden können gilt dies NICHT für nicht-symmetrische Kräfte, Momente und Verschiebungen.
Es gilt grundsätzlich:
Die Verformung der Secondary Surface folgt der Verformung der Primary Surface in Bezug auf die Symmetrieachse
Gültige Kräfte, Momente, Verschiebungen,Verdrehungen:
CF1, CM1,U1,UR1 : Nein
CF2,CM2,U2,UR2 : Nein
CF3,CM3,U3,UR3 : Ja
Die aufgebrachte Schraubenkraft wirkt in 3-Richtung.
Kräfte und/oder Momente müssen in Bezug auf das Vollmodell
durch die Anzahl der Sektoren geteilt werden !
Zur Ermittlung der Steifigkeiten müssen die Reaktionskräfte/Reaktionsmomente
mit der Anzahl der Sektoren multipliziert werden !
Beim Post-Processing kann in den ODB-Displayoptionen der Sektor auf ein volles 3D-Modell erweitert werden
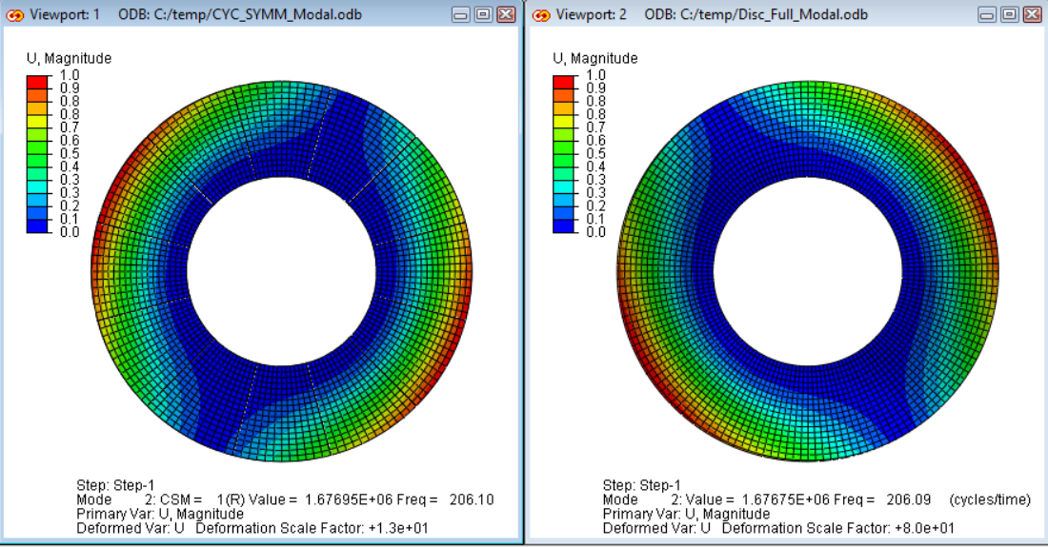
Die Berechnungen des Modells mit zyklischer Symmetrie und einem Vollmodell sollen miteinander verglichen werden.
Für die Vernetzung wurden überwiegend (bis auf die Schraube) C3D8I Elemente verwendet. Es ergibt sich wegen leichter Unterschiede der Vernetzung nicht ganz ein Faktor 12 bei der Zahl der Elemente
1/12-Modell / Zyklische Symmetrie
Vollmodell
Die von Mises Spannungen unterscheiden sich nur minimal.
1/12-Modell / Zyklische Symmetrie
Vollmodell
Durchgeführt wurden die Berechnungen auf einem Laptop (HP Z- Book, 4 Kerne, 32 Gb RAM mit GPU-Unterstützung). Es ergeben sich Unterschiede in Rechenzeit und Memory (CPU RAM) Bedarf mit einem Faktor > 12. Beide Modelle skalieren aber ähnlich.
1/12-Modell / Zyklische Symmetrie
Vollmodell
1/12-Modell / Zyklische Symmetrie
Vollmodell
Für die Darstellung der Eigenformen muss in den ODB-Displayoptionen diese Einstellung angewählt werden
1/12-Modell / Zyklische Symmetrie (Links) und Vollmodell (Rechts)
Wenn sich Randbedingungen auf der Secondary Surface der Zyklischen Symmetrie befinden wird eine Warnmeldung ausgegeben. Die Randbedingungen werden automatisch von Abaqus/CAE deaktiviert, sie können aber auch vom Benutzer deselektiert werden.
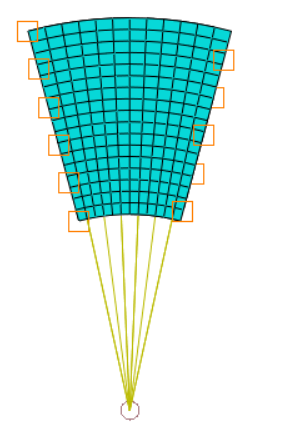
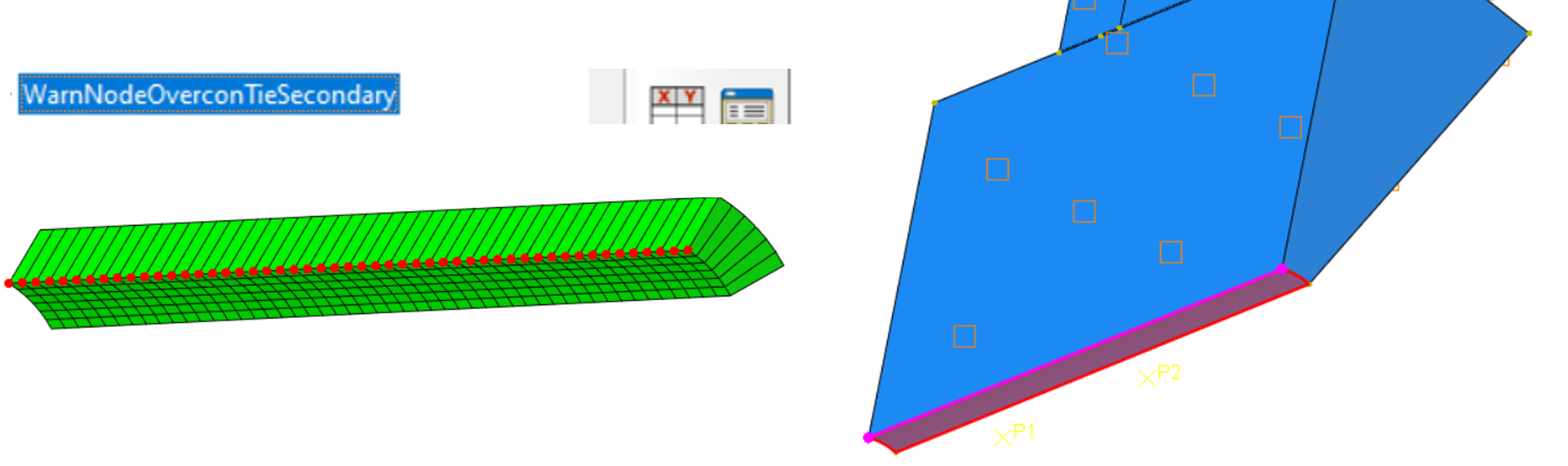
In dem Beispiel 1 werden jedoch Knoten der Secondary Surface in einem Knoten-Coupling eingesetzt, siehe Bild unten.
Wenn sich Knoten einer Knoten-Kopplung auf der Secondary Surface der Zyklischen Symmetrie befinden wird eine Warnmeldung ausgegeben. Diese Knoten werden automatisch von Abaqus/CAE aus der Kopplung entfernt, sie können aber auch vom Benutzer deselektiert werden.
Hier: Randbedingungen auf Innenfläche der Welle überschneiden sich mit Secondary surface.
