Ein Ziel vieler Simulationen ist die korrekte Berechnung der Spannungen der Bauteile unter Last. In einem Beitrag, Elementauswahl und Diskretisierung in Abaqus, haben wir uns bereits mit der Auswahl der Elemente und der Feinheit der Vernetzung beschäftigt. Die berechneten Spannungen hängen aber auch von der „richtigen“ Auflösung der Bauteilgeometrie ab. Diesem Thema wollen wir uns in dem hier folgenden Beitrag widmen.
Als Beispiel verwenden wir eine Filtertasse, wie man diese zum Beispiel Web findet. Einer Website, [4], haben wir das rechts stehende Bild entnommen. Die Filtertasse ist das gelbe Bauteil.
Die Filtertasse haben wir idealisiert und als Abaqus Modell aufgebaut.
Unsere idealisierte Filtertasse weist Symmetrien auf, links im Bild unten. Wir nutzen diese Symmetrien, indem wir nur einen Ausschnitt aus dem Modell für die Simulationen verwenden, rechts im Bild unten.
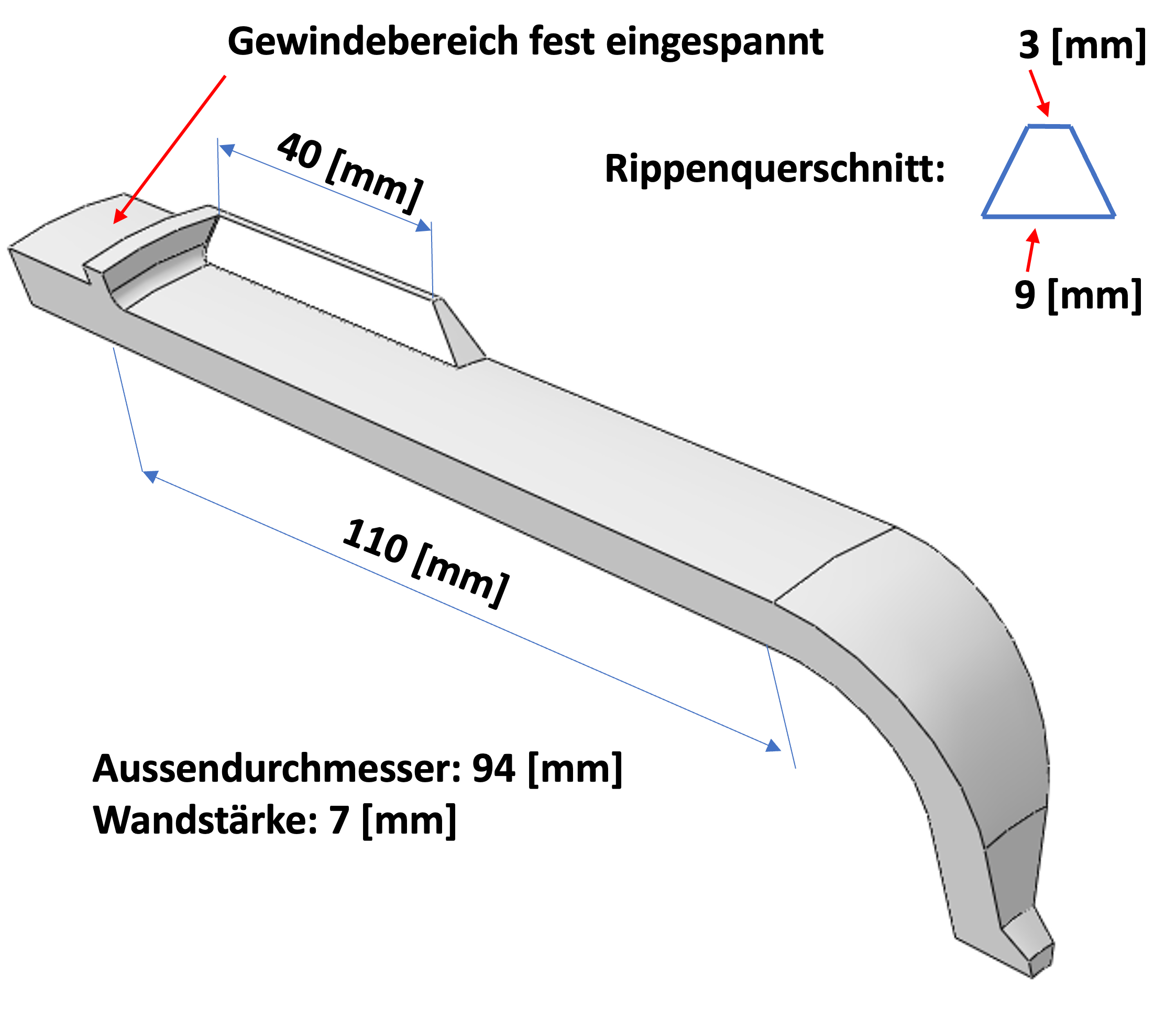
Für die Idealisierung der Filtertasse nutzen wir die im Bild unten angegebenen Abmessungen.
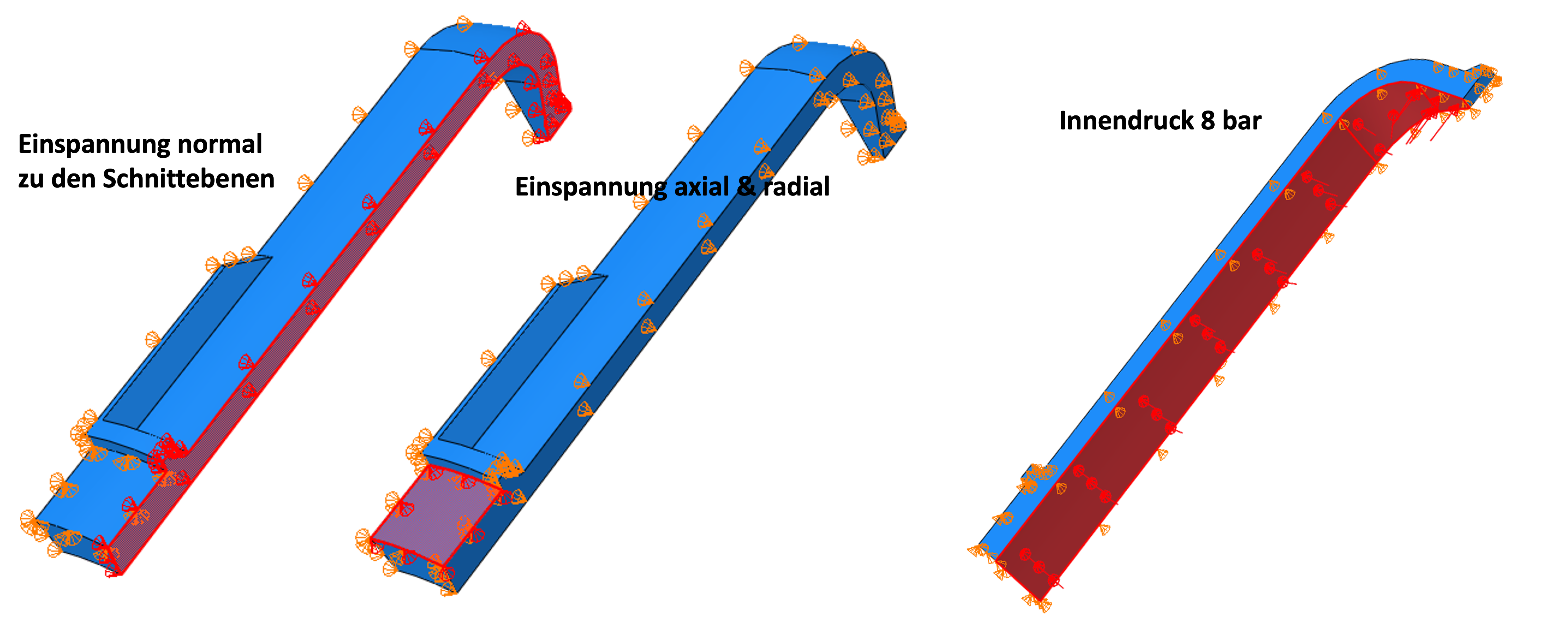
An den Schnittflächen müssen die Randbedingungen (Einspannungen) korrekt definiert werden. Über die in [1| beschriebene Vorgehen mittels der Transformation in ein lokales Koordinatensystem werden die Randbedingungen für die Knoten definiert. In diesem Fall wurde ein zylindrisches Koordinatensystem (radial R=x1, tangential θ=y1, axial Z=z1) gewählt und die Flächen in Umfangsrichtung fixiert. Zusätzlich wurde der obere Rand, welcher durch das Gewinde gehalten wird, radial und axial eingespannt. Die verwendeten Einspannungen sind links im Bild unten zu sehen. Als Last verwenden wir einen Innendruck von 8 bar, rechts im Bild unten.
Die radialen Einspannungen sind in diesem Fall gleichwertig zur Verwendung einer zyklischen Symmetrie. Einen entsprechenden Vergleich liefert der Abschnitt Wissenswertes in diesem Beitrag.
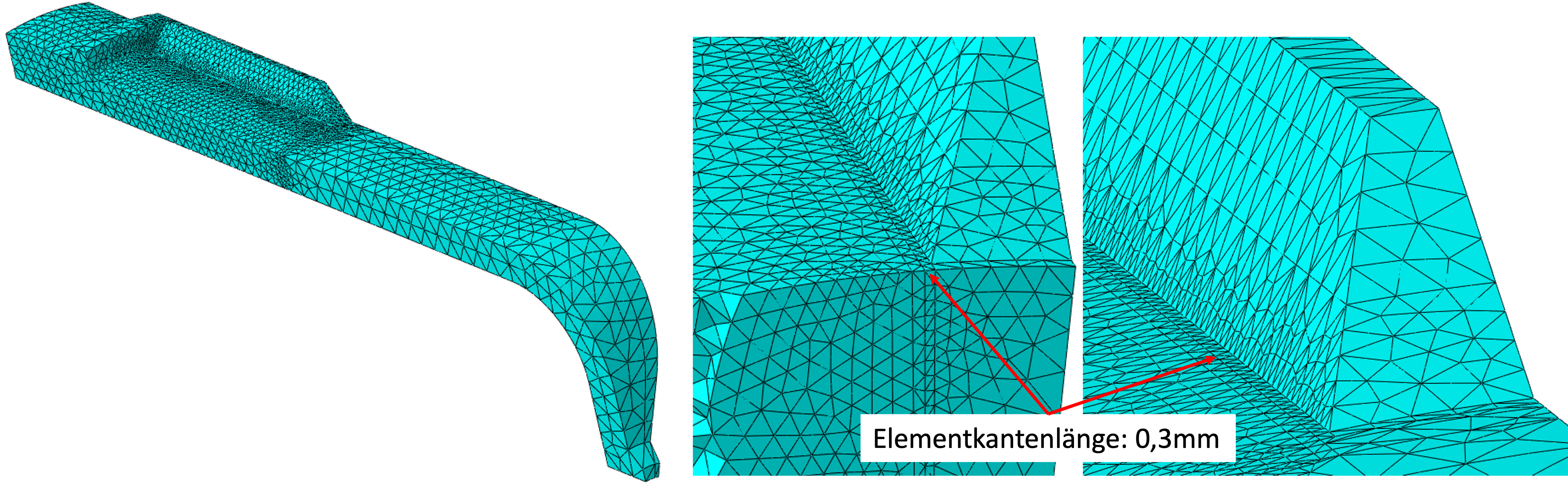
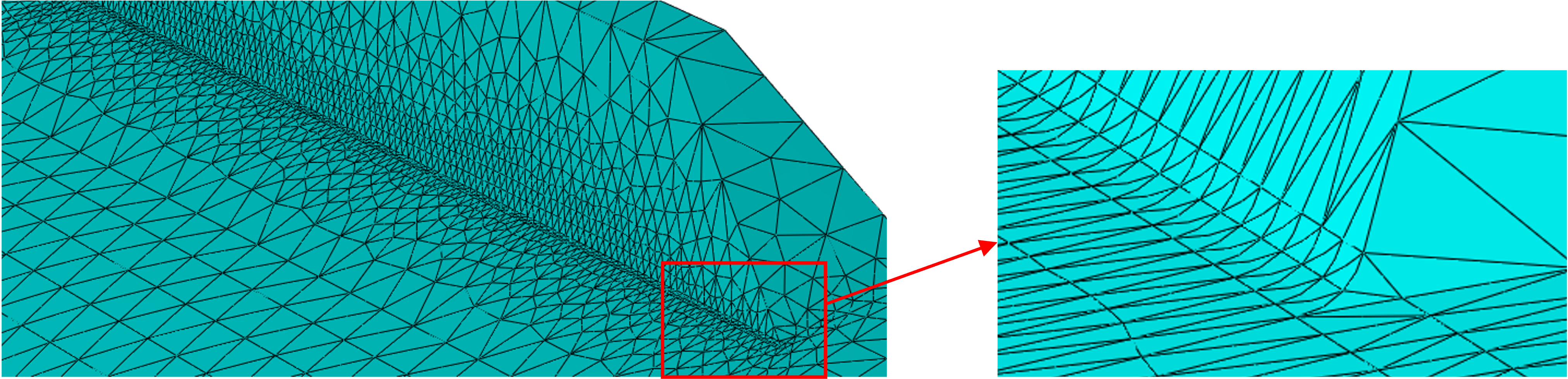
Für die Vernetzung wurden quadratische Tetraeder (C3D10) mit einer allgemeinen Elementkantenlänge von 2 mm verwendet. Im Vorfeld zu erwartende kritische Bereiche wurden nicht gesondert beachtet, d.h. nicht feiner vernetzt. Aufgrund der Geometrie und ohne Verwendung von Partitionen ist eine Vernetzung in Abaqus/CAE mit (quadratischen) Tetraedern zwingend, siehe Bild unten.
Verwendet wird als Step ein Static, General mit NLGEOM=YES. Die Last wird linear über den Belastungsschritt bis auf den Zielwert erhöht.
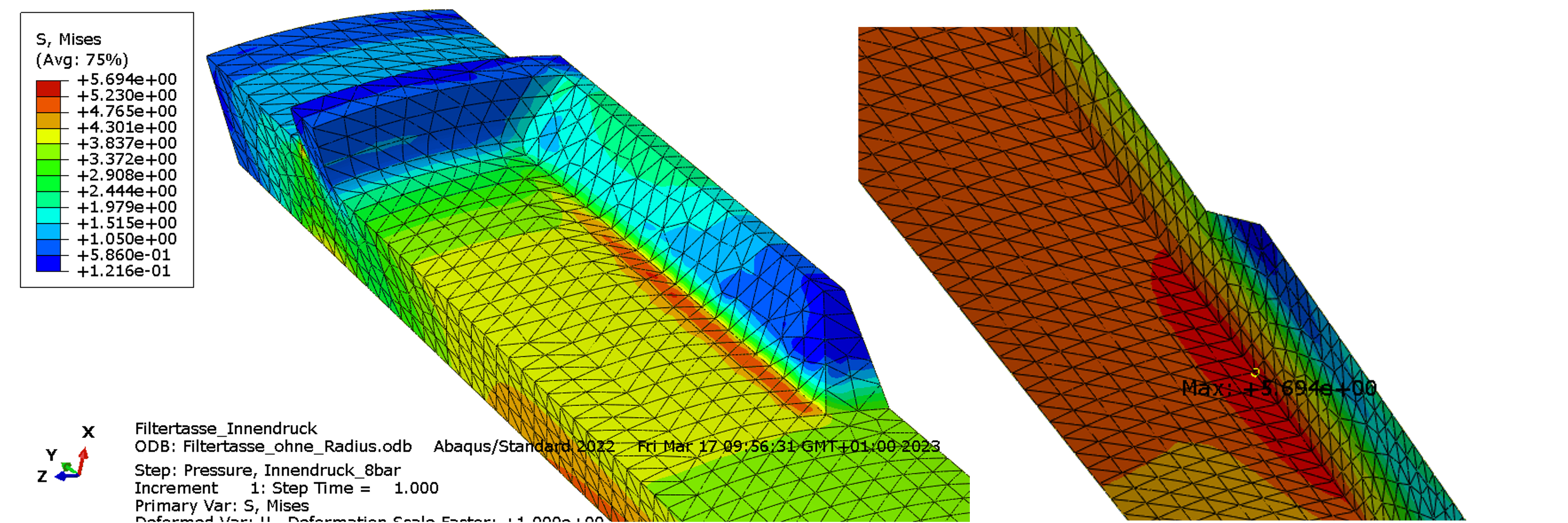
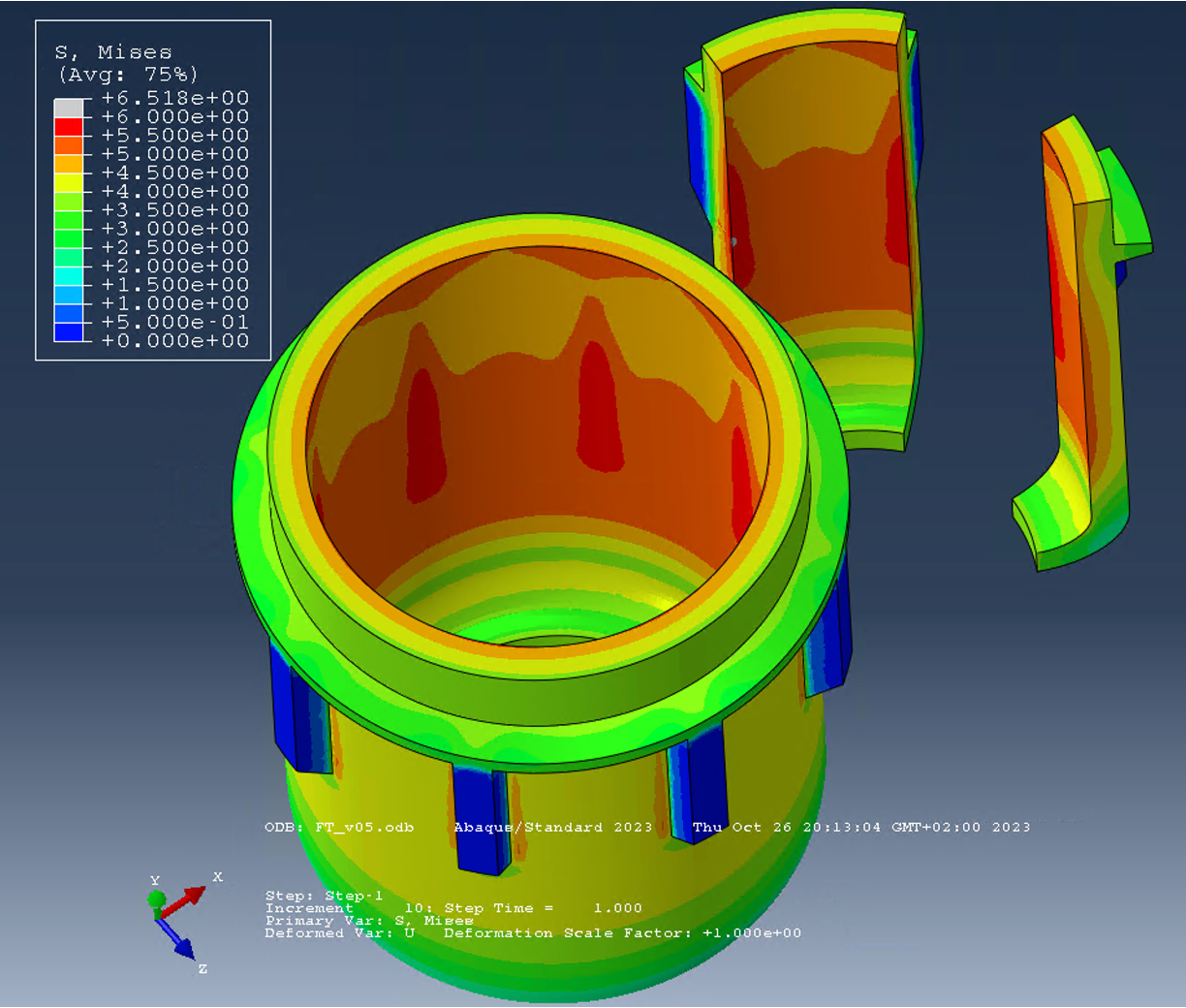
Bei Erreichen der Last beträgt die maximale Vergleichsspannung (MISES) 5.7 MPa, Bild unten. Das Spannungsmaximum befindet sich auf der Innenseite. Am Fuß der Rippe in axialer Richtung wird eine Spannungskonzentration angezeigt, welche aber etwas niedriger ist.
An dieser Stelle könnten wir unsere Arbeit nun beenden. Wir sind aber neugierig und wollen den Einfluss einer anderen Auflösung der Geometrie an der axialen Rippe untersuchen. Hierzu variieren wir unser Modell in zwei Schritten. Zum Einen setzen wir am Fuß der Rippe ein Element mit deutlich geringerer Kantenlänge quer zur Rippe. Zum Anderen modellieren wir einen Radius in den Fuß der Rippe.
Im ersten Ergebnis stellten wir eine Spannungskonzentration am Fuß der Rippe aber nicht auf der Rippe fest. Entsprechend der Darstellung im Bild unten variieren wir die Kantenlänge der Elemente, die direkt an den Fuß anschließen. Um die Längen der Elementkanten lokal verändern zu können, haben wir die Zelle in diesem Bereich partitioniert. Zuerst verwenden wir eine Kantenlänge von 0.3 mm.
Die Vergleichsspannung auf der Innenseite weist weiterhin 5.7 MPa auf. Am Fuß der Rippe steigt die Spannung allerdings nun auf 7.73 MPa, siehe Bild unten. Das Spannungsmaximum befindet sich folglich nicht mehr auf der Innenseite.
In einem nächsten Schritt verwenden wir eine Elementkantenlänge von 0.03 mm, links im Bild unten. Die maximale Spannung am Fuß der Rippe steigt nun auf 18.7 MPa, rechts im Bild unten.
Durch die einfache Variation der Elementkantenlänge und somit einer besseren Auflösung des Überganges von Rippe zu Grundkörper verschiebt sich das Spannungsmaximum von der Innenseite an den Fuß der Rippe auf der Außenseite. Zusätzlich steigt das Maximum in Abhängigkeit der Elementkantenlänge deutlich.
Übergänge mit einer Kante sind im Maschinenbau eher selten anzutreffen. Wir variieren deshalb unser Modell und verwenden einen Radius im Übergang von Rippe zur Außenfläche. Hierbei halten wir den Radius von 0.2 mm, siehe Bild unten, in den folgenden Berechnungen konstant.
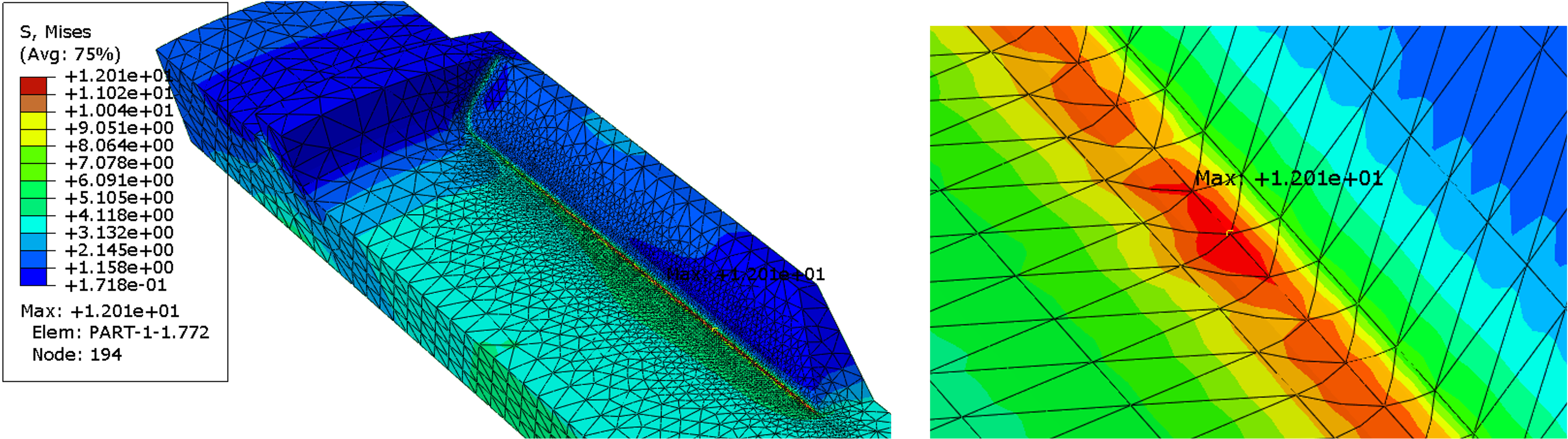
Über die Kante im Radius variieren wir die Zahl der Elemente senkrecht zur Rippe. In dem ersten Fall verwenden wir 2 Elemente. Die maximale Vergleichsspannung erhöht sich auf 12.01 MPa, siehe Bild unten.
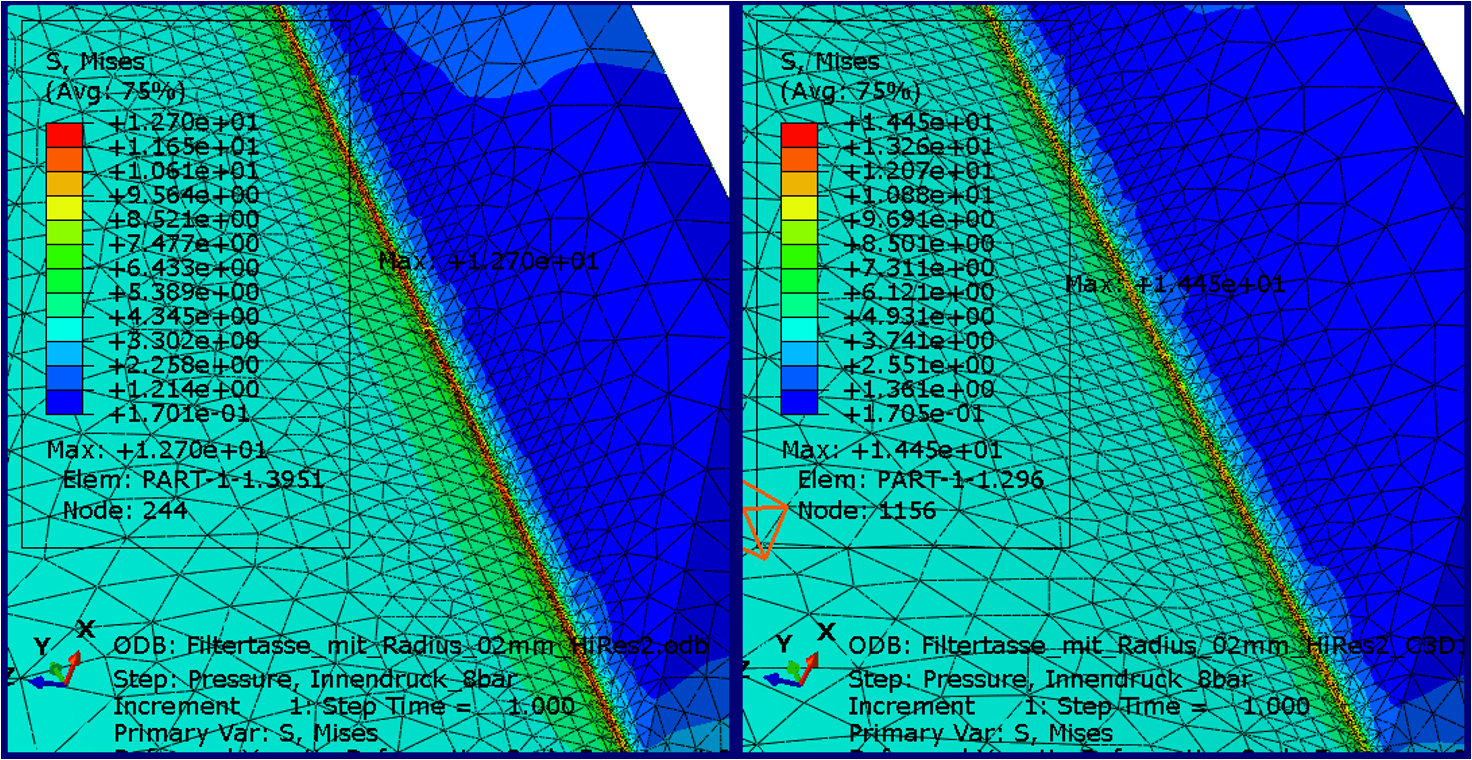
In dem zweiten Fall verwenden wir 4 Elemente. Die maximale Vergleichsspannung erhöht sich auf 12.7 MPa (also um knapp 5%), siehe Bild unten.
Nun variieren wir noch den verwendeten Elementtyp. Seit einigen Jahren stellt Abaqus Unified FEA Solid-Elemente mit einer verbesserten Beschreibung der Oberflächenspannungen (improved surface stress) dem Anwender zur Verfügung. Allerdings sind diese für Tetraeder nur zusammen mit der hybriden Beschreibung (linearer Druck) vorhanden (C3D10HS), welche das Ergebnis ebenso beeinflussen kann. Die maximale Spannung erhöht sich noch einmal, nun auf 14.45 MPa, Bild unten.
Die Einführung eines Radius führt zu einer deutlichen Erhöhung der maximalen Vergleichsspannung gegenüber der ursprünglichen Lösung. Auch die Variation des Elementtyps mit einer besseren Abbildung von Oberflächenspannungen führt zu einem anderen Ergebnis.
Die bei Belastungen auftretenden Spannungen sind ein wesentliches Maß zur Beurteilung der Qualität eines Bauteils. An dem einfachen Beispiel einer Filtertasse unter Innendruck wollten wir aufzeigen, daß maximale Vergleichsspannungen bei unterschiedlicher geometrischer Auflösung durchaus deutlich variieren können.
Zuerst verwenden wir eine durchaus plausible homogene Netzkantenlänge von 2 mm. Die maximale Vergleichsspannung findet sich auf der Innenseite und beträgt 5.7 MPa. Wir erkennen zusätzlich ein Spannungsmaximum am Fuß der axialen Rippen auf der Außenseite. Durch Verwendung eines feineren Netzes in diesem Bereich und, alternativ, durch die Einführung eines Übergangsradius verändern sich die Ergebnisse deutlich. Die maximalen Vergleichsspannungen liegen nun im Übergangsbereich der Rippen und können höhere Werte (bis zu 300%) erreichen.
Neben der Feinheit der Vernetzung und der Wahl des Elementes beeinflusst die Auflösung der Bauteilgeometrie das Ergebnis. Der Benutzer ist aufgefordert, diese Einflussgrößen zu beachten. Gerne unterstützen wir dabei.
Wie oben beschrieben nutzen wir in diesem Beispiel die Symmetrie um die Rotationsachse, um die Modellgröße zu beschränken. Wie wir in dem Beitrag Zyklische Symmetrie in Abaqus FEA beschrieben haben, bietet sich hier die Verwendung der zyklischen Symmetrie an. Ein Vorteil der Verwendung der zyklischen Symmetrie ist der Umstand, daß sich der Verwender keine Gedanken zu den Randbedingungen in Umfangsrichtung machen muss. In diesem Fall haben wir uns anders entschieden. Um nachzuweisen, daß die verschiedenen Abbildungen gleichwertig sind, haben wir ein entsprechendes Beispiel erstellt. In diesem Beispiel haben wir ein Vollmodell mit einem 1/8 Modell unter Verwendung der zyklischen Symmetrie und mit obigen 1/16 Modell verglichen. Auch in diesem Beispiel haben wir quadratische Tetraeder (C3D10) und die ursprüngliche, homogene Vernetzung verwendet. Im unterstehenden Bild erkennt man, dass alle Modelle gleichwertige Ergebnisse liefern.
Nicht gleichwertig ist der numerische Aufwand für die unterschiedlichen Modelle. Im Bild unten haben wir die Anzahl der Variablen, die Rechenzeit und den notwendigen Speicher (RAM) miteinander verglichen. Es zeigt sich, daß es sich lohnen kann, reale Symmetrien in Modellen zu verwenden. Dies aber bitte nur dann, wenn sichergestellt ist, daß die Problemstellung die Verwendung von Symmetrien zulässt.
Nur kurz wollen wir einen Vergleich mit der Kesselformel ziehen. Ausführliche Erklärungen finden sich in [2] und in englischer Sprache in [3]. Bei dem obigen Beispiel gilt es zu beachten, daß das Verhältnis von Durchmesser zu Wanddicke nicht den Bedingungen der Kesselformel genügt. Die Randbedingungen entsprechen auch nicht denen eines Kessels. Gut vergleichbar ist deswegen hier nur die tangentiale Spannung.
Unter Verwendung obiger geometrischer Werte mit einem mittleren Durchmesser dm=87 mm sowie einer Wanddicke von s=7 mm und einem Druck von 0,8 MPa, so ergibt sich nach der Kesselformel eine tangentiale Spannung von 4,97 MPa, Formel und Abbildungen aus [2] im Bild unten. Dies entspricht recht gut den Werten der tangentialen Spannung in unserem Beispiel.
Zum Teil basiert der vorliegende Text und gezeigter Abbildungen auf der Recherche ausgewerteter Literatur. Ist dies der Fall, so werden die Quellen im Text durch eine Zahl, z.B. [2], gekennzeichnet und die Quelle hier aufgeführt.
Zum Teil sollen die hier aufgeführten Quellen aber auch einfach nur als Empfehlung weiterführender Literatur verstanden werden.