Abaqus bietet eine große Auswahl an Elementen für die verschiedenen Analysen an. Hilfestellung zur richtigen Auswahl der Elemente bieten das Handbuch, [1], und Axel Reichert in [2].
Ein kleines Beispiel zeigt, dass es immer auf den Anwendungsfall und die Ziele einer Berechnung ankommt, welcher Elementtyp und welche Diskretisierung eingesetzt werden sollen. Bei dem hier dargestellten, kleinen Beispiel eines Biegebalkens mit punktförmiger Biegekraft handelt es sich um einen linearen (Geometrie und Material) Fall der Strukturmechanik. Das Beispiel soll darstellen, wie sich die Ergebnisse in Abhängigkeit vom gewählten Element und der Diskretisierung verändern. Betrachtet wurde dabei bisher nur Hexaeder Elemente.
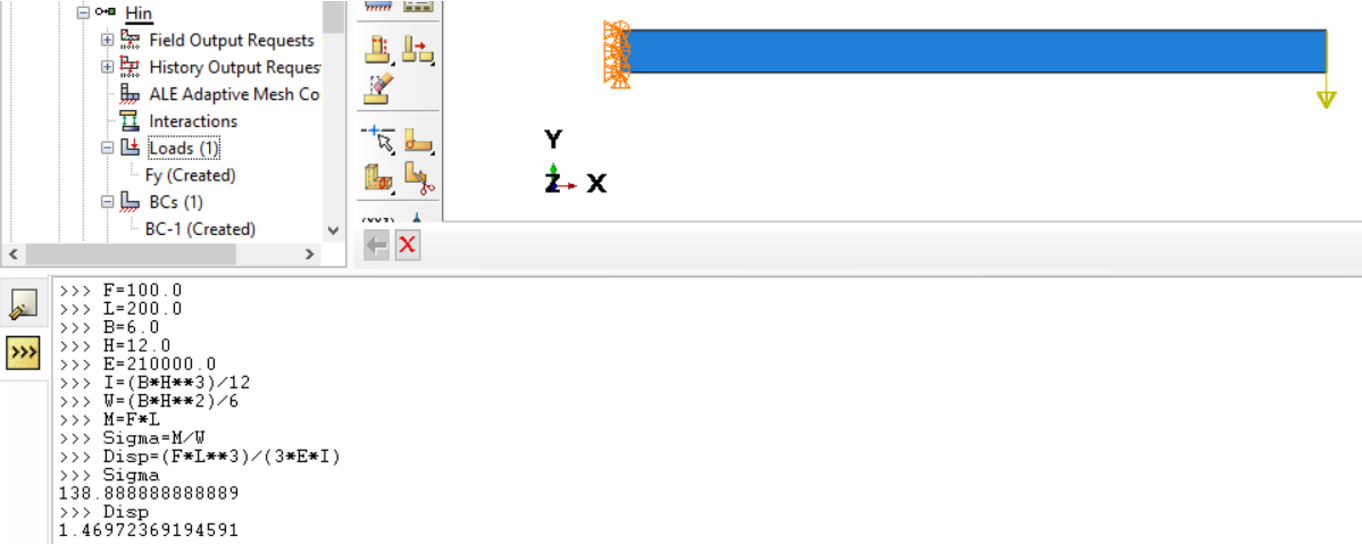
Der Biegebalken, 200 mm lang, 6 mm breit und 12 mm hoch (siehe Bild unten), wird an dem einen Ende in x- und y-Richtung sowie in der Mittelebene in z-Richtung gehalten. Die Form der Einspannung soll das Auftreten von Spannungsspitzen an der Einspannung reduzieren. Als Material wird Stahl verwendet. Die Last wird an den oberen beiden Ecken des anderen Endes punktförmig aufgebracht (F = 2 x 50 N). Analytisch wird die Verschiebung in y-Richtung (u2) und die Biegespannung (entspricht S11) an der Einspannstelle bestimmt. Für die Berechnung der analytischen Lösung kann auch die Konsole (Kernel Command Line Interface) von Abaqus/CAE verwendet werden.
Es werden 4 Parts des gleichen Biegebalkens verwendet, um die Ergebnisse verschiedener Elementtypen gleichzeitig betrachten zu können,
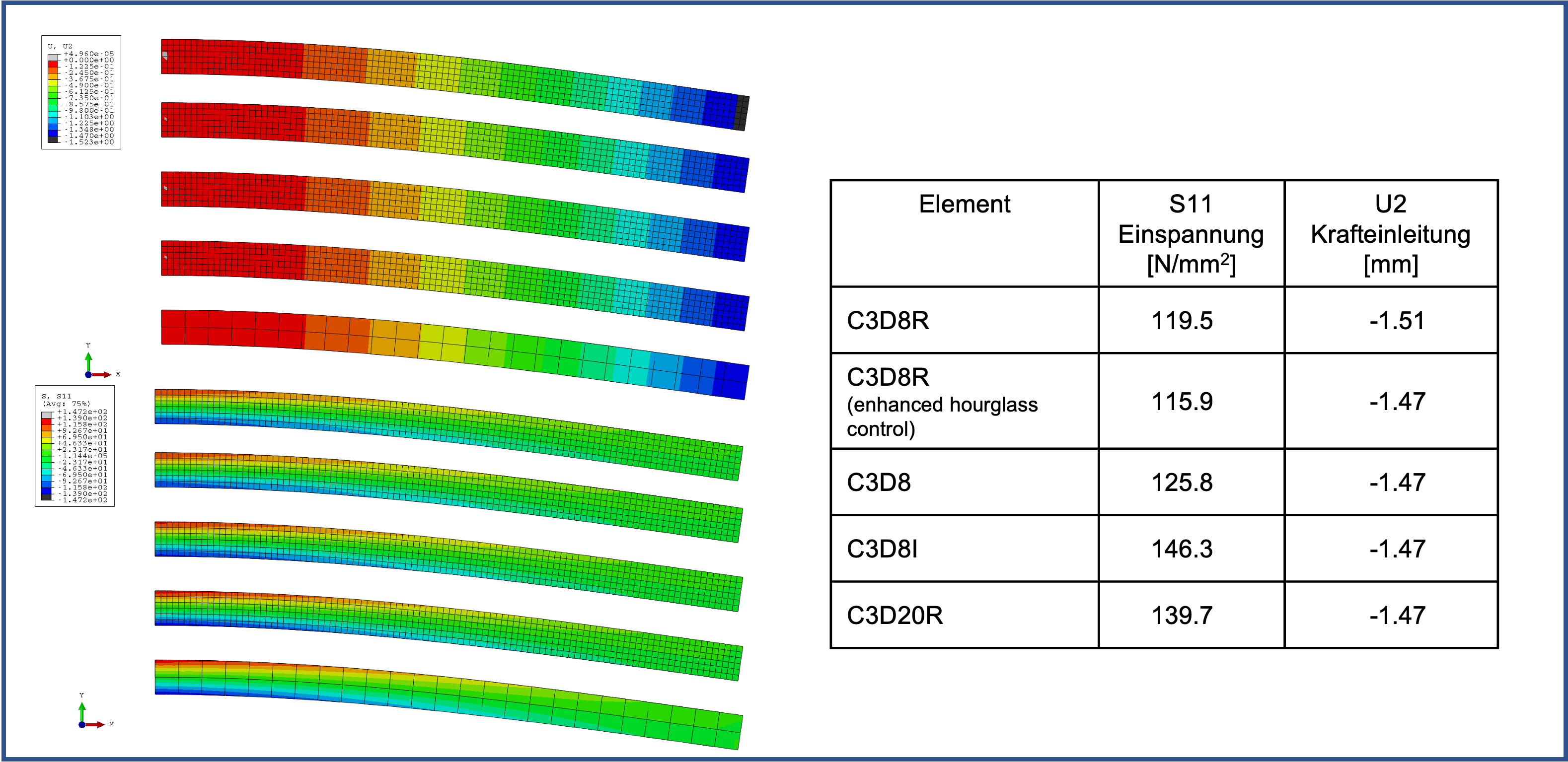
Verwendet wurden die Elementtypen (von oben nach unten) C3D8R, C3D8R mit Enhanced Hourglass Control, C3D8 und C3D8I.
- C3D8R: 8 Knoten lineares Hexaederelement mit reduzierter Integration (1 Integrationspunkt / Element )
- C3D8R: wie oben, mit Enhanded Hourglass Control
- C3D8 : 8 Knoten vollintegriertes Hexaederelement (8 Integrationspunkte / Element )
- C3D8I : 8 Knoten modifiziertes vollintegriertes Hexaederelement ( 8 Integrationspunkte / Element )
(siehe auch [3])
Alle Berechnungen wurden mit Abaqus/Standard v2022 HF6 durchgeführt. Verwendet wurde ein Static General Step, wobei NLGEOM = OFF gesetzt blieb.
Vergleicht man Verschiebungen und/oder Spannungen zwischen analytischer und numerischer Lösung, so ergibt sich immer das Problem, an welchen Punkten verglichen werden soll. Verschiebungen werden an den Knotenpunkten berechnet und können dort direkt abgelesen werden. Spannungen (und Dehnungen) werden aber an den Integrationspunkten berechnet. Diese liegen aber nicht an den Oberflächen der Elemente und so ist hier ein Vergleich direkt nicht möglich. Hier verwenden wir die auf die Knoten an der Oberfläche extrapolierten Werte, woraus sich immer ein gewisser Fehler ergibt.
Für die verschiedenen Element-Typen wurde jeweils die Elementgröße des Modells (über die Angabe in Mesh/Seed/Part) variiert.
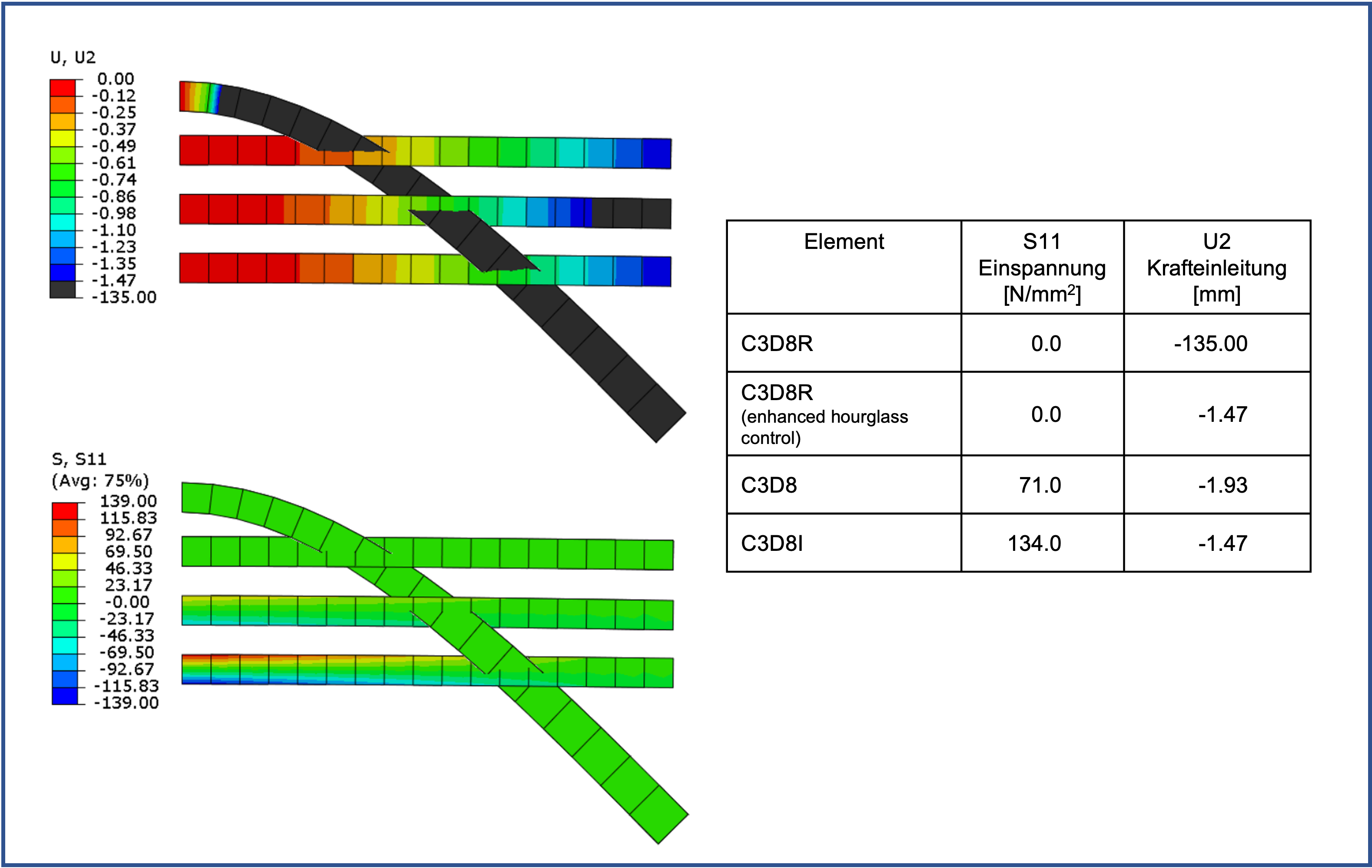
Bei recht sparsamer Diskretisierung mit einer Kantenlänge von 12 mm kann mit einem Element über die Höhe des Balkens der Spannungsverlauf durch die Biegung nicht abgebildet werden.
Zudem verhält sich das reduziert integrierte Element mit Default Hourglass Control sehr weich. Nur das C3D8I Element liefert hier ein brauchbares Ergebnis.
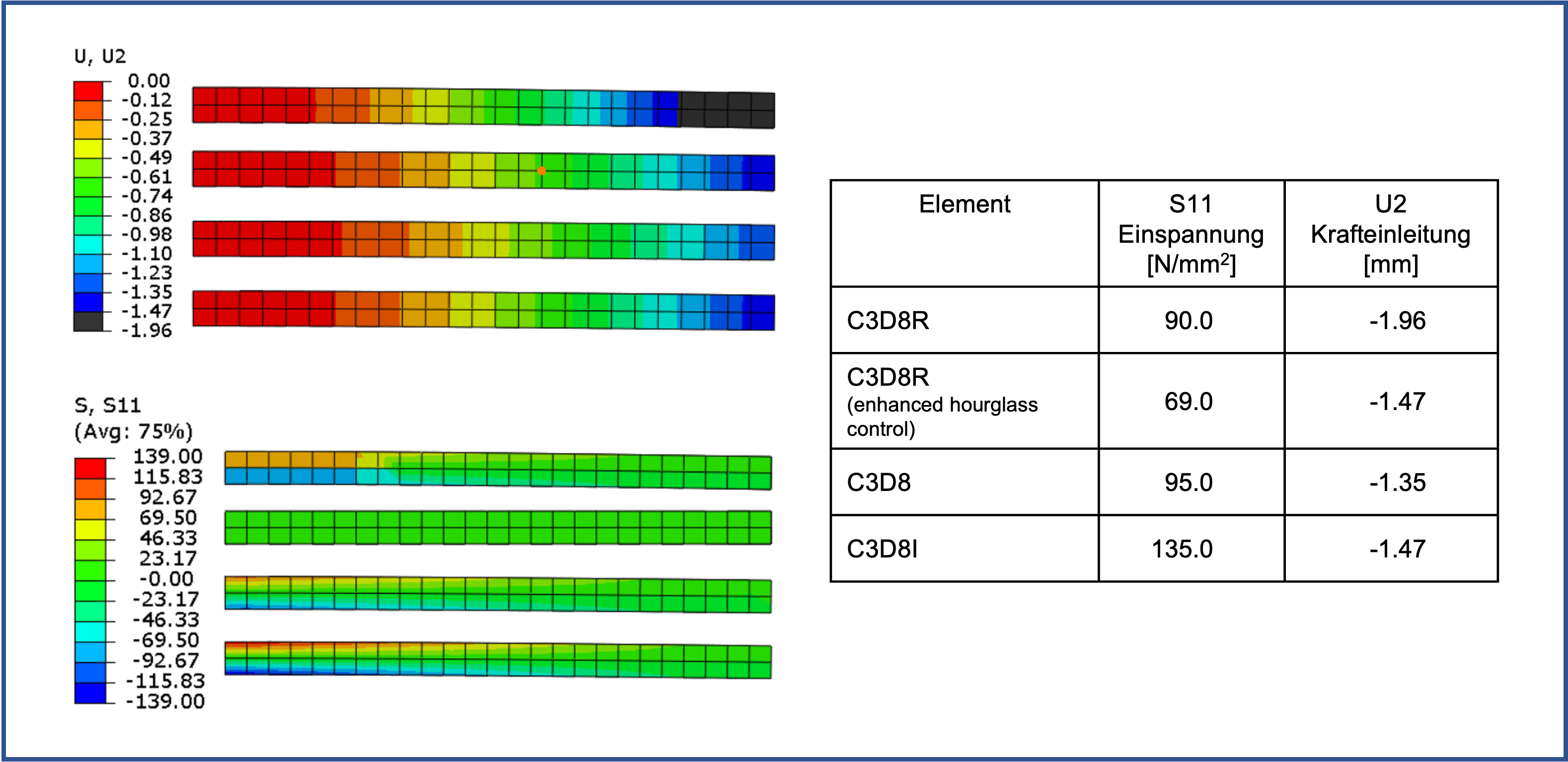
Bei einer Kantenlänge von 8 mm und somit 2 Elementen über die Höhe ergibt sich ein ähnliches Ergebnis:
Einzig das C3D8I Element weist ein brauchbares Ergebnis aus.
Bei einer Kantenlänge von 4 mm und somit 3 Elementen über der Höhe werden die Ergebnisse hinsichtlich der Verschiebungen deutlich besser.
Allerdings wird das Spannungsbild weiterhin schlecht dargestellt.
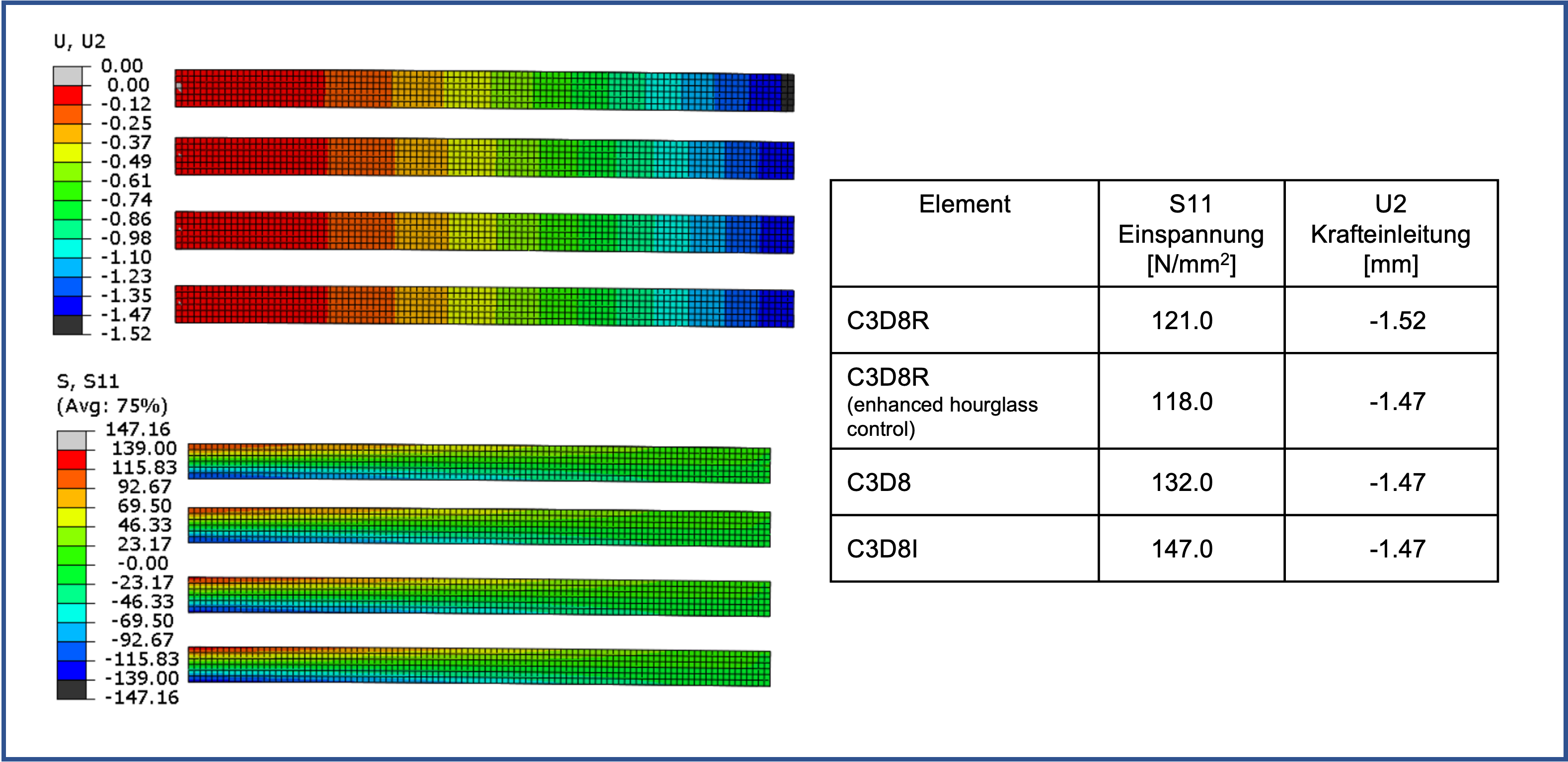
Erst bei einer Kantenlänge von 2 mm und somit 6 Elementen ergibt sich eine weitere Verbesserung.
Allerdings stellen die reduziert integrierten Elemente weiterhin das Spannungsbild nicht korrekt dar.
Dieses kleine Beispiel stellt dar, dass bei „falscher“ Elementwahl auch eine vermeintlich einfache Problemstellung hinsichtlich der Spannungsbewertung nicht korrekt wieder gegeben wird. Hier stellt das C3D8I Element das Mittel der Wahl dar, wenn man nicht auf quadratische Elementansätze wechseln will.
Es sei nicht unerwähnt, dass in Abaqus/CAE das C3D8R Element als Voreinstellung verwendet wird. Sicherlich hat dieses Element bei nicht linearen Berechnungen und großen Deformationen seine Vorteile, bei der hier gezeigten linearen Anwendung und kleinen Deformationen aber nicht.
Grundsätzlich wollen wir uns weiter diesem Thema widmen.
Ein kurzer Test mit C3D20R zeigt, dass auch bei deutlich gröberer Diskretisierung eine gute Ergebnisqualität erreicht werden kann.
Das Element für alle Finite Element Berechnungen gibt es leider nicht. So sollte der Anwender in Abhängigkeit von der zu berechnenden Problemstellung und den Zielen einer Berechnung das „richtige“ Element und die richtige Diskretisierung selbst bestimmen. Unterstützt wird der Anwender durch das Handbuch der Software und durch einzelne Beiträge verschiedener Autoren. Mit diesem Beitrag wollen wir darlegen, wie stark die Ergebnisse einer einfachen lineare Berechnung eines Biegebalkens von der Wahl des Elementtyps und der Diskretisierung abhängen können. In diesem einfachen Fall sind C3D8I oder C3D20R das Mittel der Wahl. Weitere Beiträge zu diesem Thema sollen noch folgen.
Zum Teil basiert der vorliegende Text und gezeigter Abbildungen auf der Recherche ausgewerteter Literatur. Ist dies der Fall, so werden die Quellen im Text durch eine Zahl, z.B. [2], gekennzeichnet und die Quelle hier aufgeführt.
Zum Teil sollen die hier aufgeführten Quellen aber auch einfach nur als Empfehlung weiterführender Literatur verstanden werden.