K-Tag 2024 – Anwendungen zur Demokratisierung der Simulation

Betrachtet man ein paar Schlagzeilen zur Simulation in diesen Tagen, so bekommt man leicht den Eindruck, daß die sofortige Integration der Simulation in die bestehenden Entwicklungsprozesse notwendig ist. Im folgenden Bild werden ein paar dieser Schlagzeilen wiedergegeben.

Nach [2] ist es wichtig, daß der „schöpferische und kreative“ Konstruktionsprozeß nicht unterbrochen wird. Dies geschah in der Vergangenheit durch das Warten auf Versuche oder das Warten auf die Simulation. In [3] wird die Simulations-Abteilung als ‚bottleneck‘ im Entwicklungsprozeß bezeichnet. In [4] führt der sequentielle Arbeitsablauf von Konstruktion-Simulation-Konstruktion zu ineffektiven Entwicklungsprozessen.

Der Begriff des Arbeitens in Silos findet sich häufig. In einem internen Dokument der Dassault Systèmes wird dieses Arbeiten in Silos bildlich dargestellt:

In den letzten Jahren gab es durch die Entwicklung der Software Systeme für die Simulation eine deutliche Verbesserung der Werkzeuge für die Simulation. Wesentliche Punkte sind dabei:

• Verbesserte Geometrie-Aufbereitung
• Automatische Vernetzung auch “schlechter” Geometrien
• Verbessertes Konvergenz-Verhalten der impliziten Solver
• Einsatz expliziter Solver für statische Problemstellungen
• Einsatz des automatischen Kontaktes zwischen Bauteilen
• Beseitigung der Schnittstellen bei Multi-Physics Anwendungen.

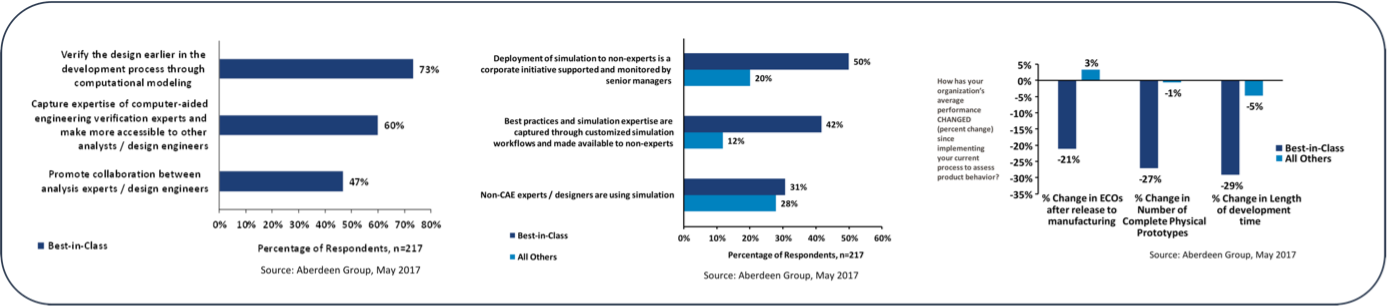
In [3] werden die Vorteile der konstruktions-integrierten Simulation für die Industrie anhand von Umfrage-Ergebnissen dargelegt. Hierbei wird zwischen innovativ führenden Firmen (Best-in-Class) und dem „Rest“ (All Others) unterschieden. Betont wird das „Left Shifting“, eine frühe Verifikation und Optimierung des Produktes, links im folgenden Bild. Ein Wechsel hin zur konstruktions-integrierten Simulation wird von vielen Firmen angestrebt, mittig im folgenden Bild. Hierdurch konnten die Firmen die Kosten und die Dauer der Entwicklungsprozesse deutlich reduzieren, rechts im Bild.

So wird nach [2] der Einsatz von Simulation im Konstruktionsprozeß deswegen besonders wichtig, da der Wechsel von einer erfahrungsbasierten zu einer wissensbasierten Entscheidung in der Konstruktion erfolgen muss. In [5] werden die Vorteile einer Konstruktions-integrierten Simulation dargestellt. Die Anforderungen an die Konstruktionsprozesse sind in einer schwierigeren Umgebung stark gestiegen. Hier ist die Konstruktions-integrierte Simulation ein Problemlöser und beschleunigt somit die Demokratisierung der Simulation.

Heutige Software-Systeme bieten entsprechende Lösungen an, siehe folgendes Bild. In [6] wird das Produkt SimSolid von der Firma Altair beschrieben. In [7] wird die Software ANSYS Discovery vorgestellt. In [8] wird der MODSIM Ansatz von Dassault Systèmes beschrieben.

In der Literatur finden sich genügend Argumente für eine deutliche Stärkung der konstruktions-integrierten Simulation. Die Demokratisierung der Simulation führt zu besseren Produkten in kürzeren Entwicklungsprozessen. Die Software-Hersteller stellen dafür die notwendigen Werkzeuge bereit, wobei zwischen geführten und neueren/automatisierten Berechnungsprozessen unterschieden werden kann.

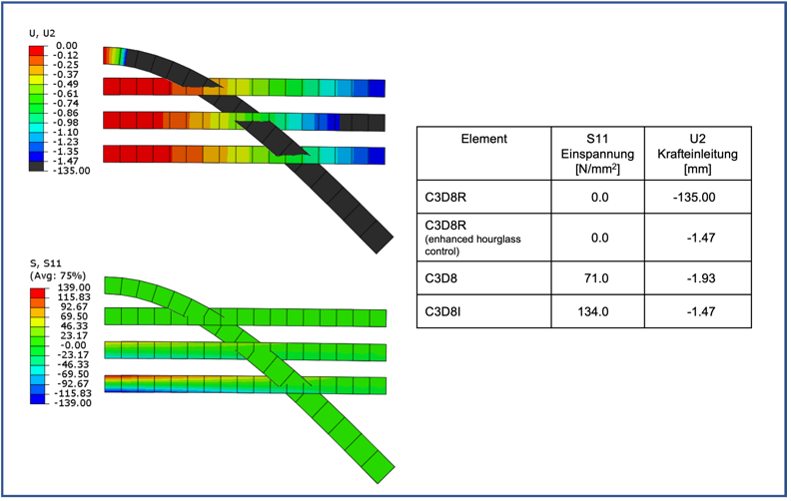
Fragt man einen erfahrenen Berechnungs-Ingenieur, so ist die Wahrscheinlichkeit hoch, daß dieser ob dieser Entwicklung starke Bedenken hat. Auf unserer Website [9], auch hier, haben wir einen Beitrag, welcher sich mit der richtigen Wahl der Elemente für eine Simulation befasst. Als Beispiel dient die lineare Belastung eines Biegebalkens. Hier zeigt sich, daß die falsche Wahl von Element und Diskretisierung zu komplett falschen Ergebnissen führen kann. In dem folgenden Bild führt nur die Wahl eines, in der Praxis eher selten verwendeten, Elementes zum richtigen Ergebnis.

In der Literatur zu den automatisierten Berechnungsprozessen finden sich Hinweise zur Verwendung von Referenz-Speicher (Reference Memory in [10]), der Treue oder des Speichers der Grafikkarte zur Erhöhung der Qualität der Berechnung [2]. Dies erscheint doch eher schwierig, da bisher keine Literatur gefunden wurde, welche die Abhängigkeit der Physik einer Simulation von solchen Größen näher definiert.

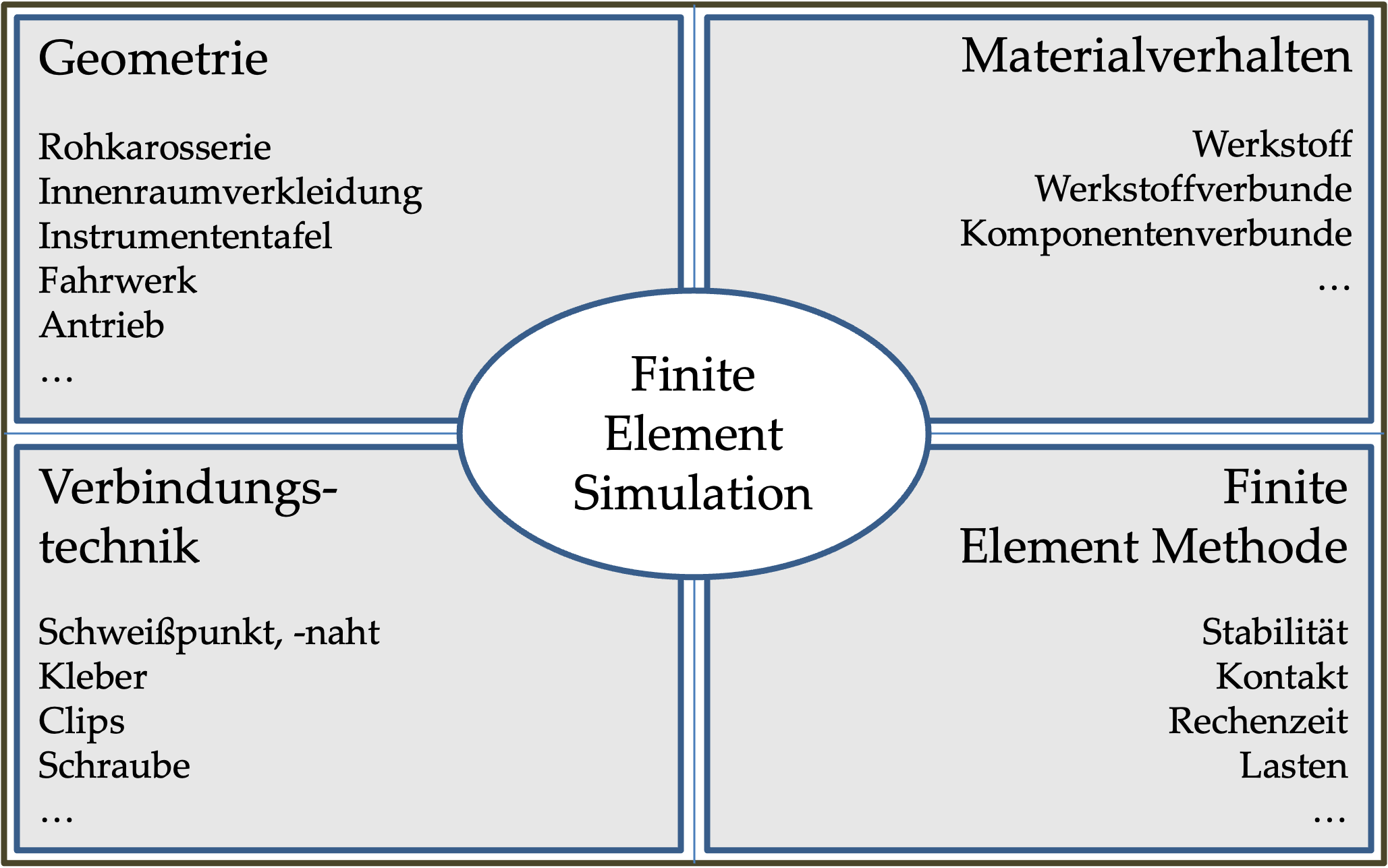
Bereits in einer früheren Veröffentlichung [11] haben wir erläutert, daß die Güte und Prognosefähigkeit einer Simulation von der Qualität der Abbildung von Geometrie, Material, Verbindungstechnik und den Algorithmen der Finite Element Methode abhängen. Folgendes Bild haben wir dieser Veröffentlichung entliehen.

Je nach qualitativen und quantitativen Zielen einer Simulation sollte die Qualität in einzelnen oder allen Bereichen geprüft und verbessert werden. Der frühere Vortrag enthält Beispiele und Vorgehensweisen zur Bearbeitung der Bereiche.

Als Beispiel verwenden wir eine einfach Welle-Nabe-Verbindung. Die Abbildung der Geometrie und gegebenenfalls einer Verbindungstechnik ist recht einfach. Meist stellt die Dimension (im m-Bereich) und die notwendige Auflösung (im mm-Bereich) eine Herausforderung, insbesondere an die verwendete Hardware, dar. Das Materialverhalten wird auf die Elastizität eines Metalls beschränkt. Die Finite Element Simulation soll Ergebnisse hinsichtlich der Mikrobewegung zwischen Welle und Nabe sowie der Spannungen im Bereich der Oberfläche der Welle liefern, welche anschließend in einer Dauerfestigkeitsberechnung verwendet werden. Obwohl Kanteneffekte wegen deren Singularität zuerst ausgeschlossen werden, bedarf es grundsätzlicher Untersuchungen zur „korrekten“ Abbildung der Mikrobewegungen und der Spannungen. Eine realistisch durchführbare Simulation erlaubt aber nur eine minimale Elementkantenlänge von circa 3 mm. Die Berechnungen wurden mit Abaqus/Standard [12] durchgeführt.

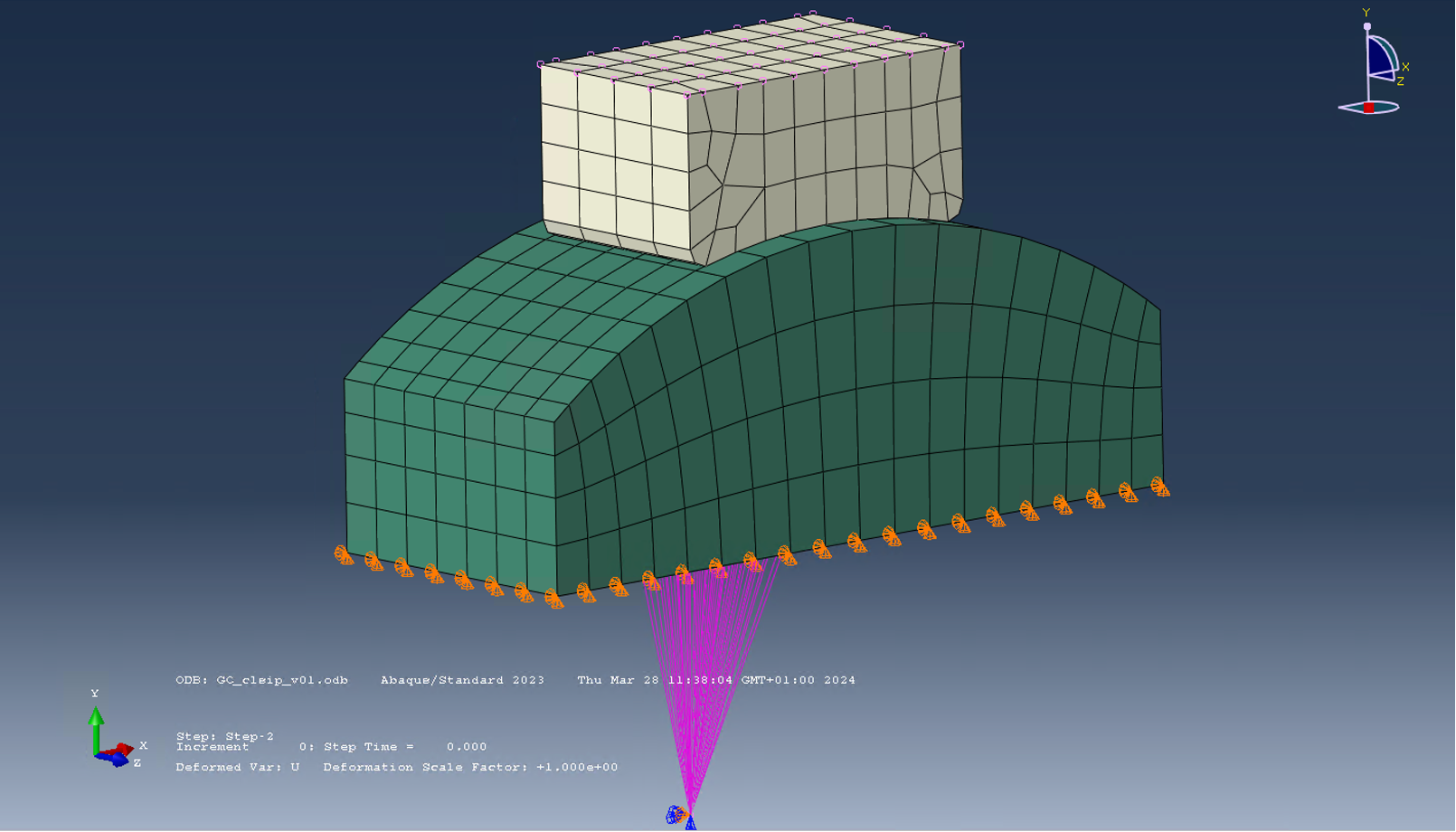
Zuerst wird ein 3-dimensionales Testmodell verwendet. Ein Bauteil (Impactor) wird gegen ein anderes Bauteil (Block) 0.03 mm gedrückt (Step-1) und anschließend um 0.01 Grad verdreht (Step-2). Aus beiden Belastungen ergeben sich geringe Relativ-Verschiebungen im Tausendstel Millimeter-Bereich. Die Mikrobewegungen sollen an der Kontaktfläche ausgewertet werden.

In Voruntersuchungen wurde bereits der zu verwendete Elementtyp festgelegt, ein voll-integriertes, lineares 8-Knoten-Solid Element (C3D8I), siehe auch [9]. Variiert wurde die Elementkantenlängen und der Elastic Slip der Penalty Formulierung für die Reibung. Hierbei handelt es sich um eine elastisch-ideal plastische Beschreibung des Reibverhaltens, um eine stabile Konvergenz zu gewährleisten. Der Elastic Slip Factor beschreibt dabei die elastische Steigung (je kleiner, desto steiler). Dieser Faktor kann relativ zur Elementkantenlänge (Elastic Slip Tolerance) oder als Dimension (Elastic Slip) definiert werden. Folgende Varianten wurde berechnet:

Man erkennt, daß die Bauteile partitioniert werden mussten, um das Modell rechenbar zu halten. Bei der v14 haben 128 GByte RAM nicht ausgereicht, so daß die Simulation extrem lange dauerte.

Für die Bestimmung der Mikrobewegung wird hier die Abaqus Variable CLSIPEQ verwendet. Diese stellt die aufsummierte resultierende Bewegung in der Kontaktebene dar. Verwendet man die Default-Parameter so erkennt man im Vergleich der Varianten v11, v12, v13 und v14 eine deutliche Abhängigkeit des Ergebnisses von der Feinheit des Netzes, siehe folgendes Bild.

Für die Varianten mit 3 mm und 1 mm Elementkantenlänge erscheint das Ergebnis noch symmetrisch. Die Verwendung der Default-Parameter erscheint somit nicht zulässig für die Detektion der Mikrobewegungen mit einer Vernetzung mit 3 mm Kantenlänge.

Es gibt hier aber eine anwendbare einfache Lösung durch die Vorgabe eines festen Elastic Slip, wie in diesem Fall, oder einer deutliche kleineren Elastic Slip Tolerance. Nun ist das Ergebnis für größere Elementkantenlängen deutlich näher an dem Ergebnis mit einem sehr feinen Netz, siehe folgendes Bild. Aufgrund der deutlichen Unterschiede in der Elementkantenlänge bleiben aber weiterhin Unterschiede, welche vernachlässigt werden müssen. Weiterführende Literatur findet sich zum Beispiel in [13].

Das gleiche Modell wird auch zur Darstellung der Spannungen in Abhängigkeit von der Elementkantenlänge verwendet. Abaqus ermöglicht die Ermittlung der Spannungen entlang eines Pfades. Schon die Darstellung dieser Pfade im folgenden Bild zeigt, daß Unterschiede in den Spannungen im Block zu erwarten sind. Allerdings gilt auch hier, daß eine minimale Elementkantenlänge von 3 mm für eine Simulation der Problemstellung notwendig sind.

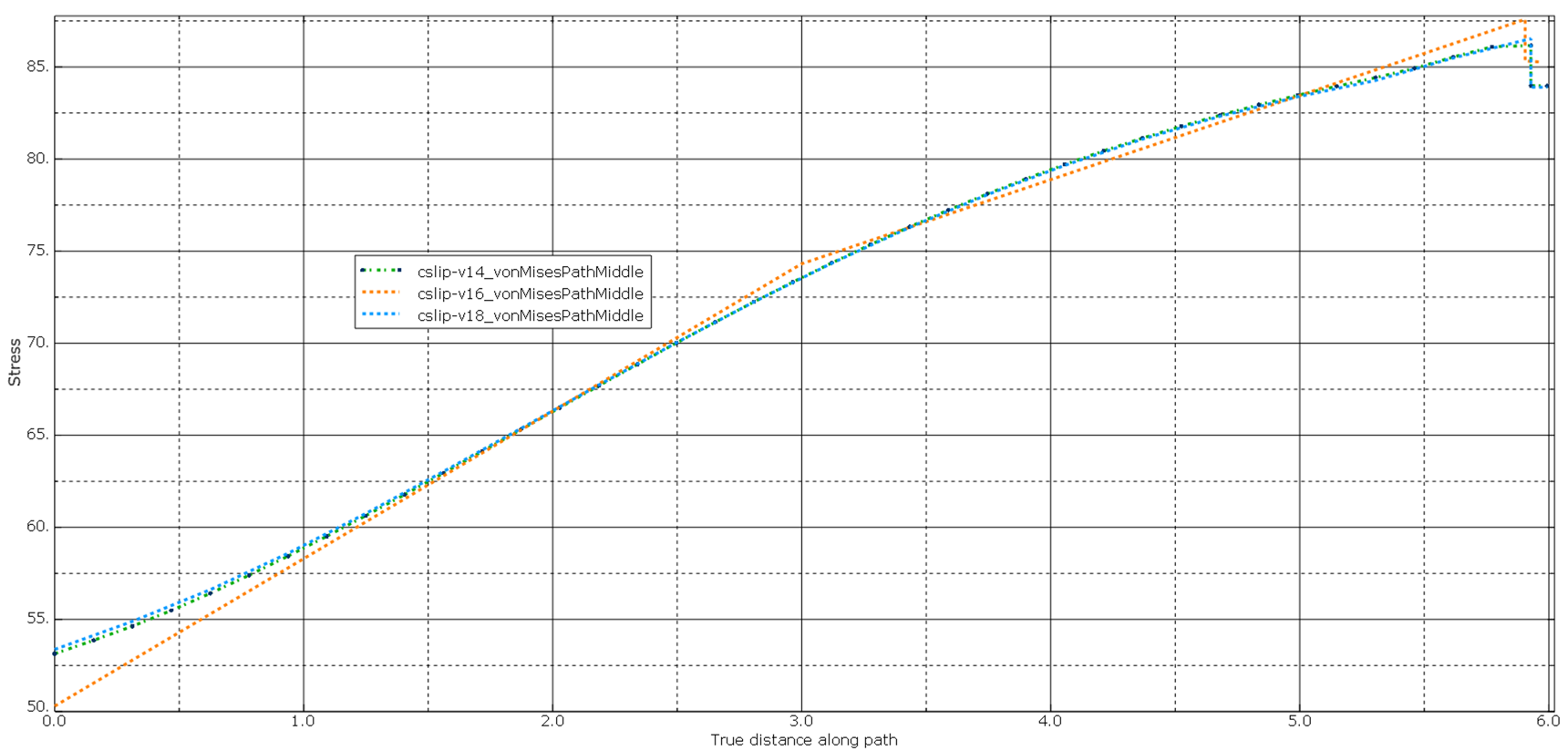
Betrachtet man nun die Spannungen entlang dieses Pfades für die Varianten v14 (0.15 mm Kantenlänge), v16 (3 mm Kantenlänge) und v18 (0.3 mm Kantenlänge) so ergeben sich folgende Spannungsverläufe entlang des Pfades (beginnend an der Oberfläche), siehe folgendes Bild. Die Abweichungen sind hier gering und können vernachlässigt werden.

Es zeigt sich an diesem kleinen Beispiel, daß mit einer Korrektur der Default-Werte für den Kontakt auch mit einem groben Netz Aussagen über Mikrobewegungen und Spannungen getroffen werden können. In diesem Fall führt die Korrektur der Default-Werte auch zu nur einer geringen Veränderung des Konvergenzverhaltens und damit des Zeitaufwandes der Simulation.

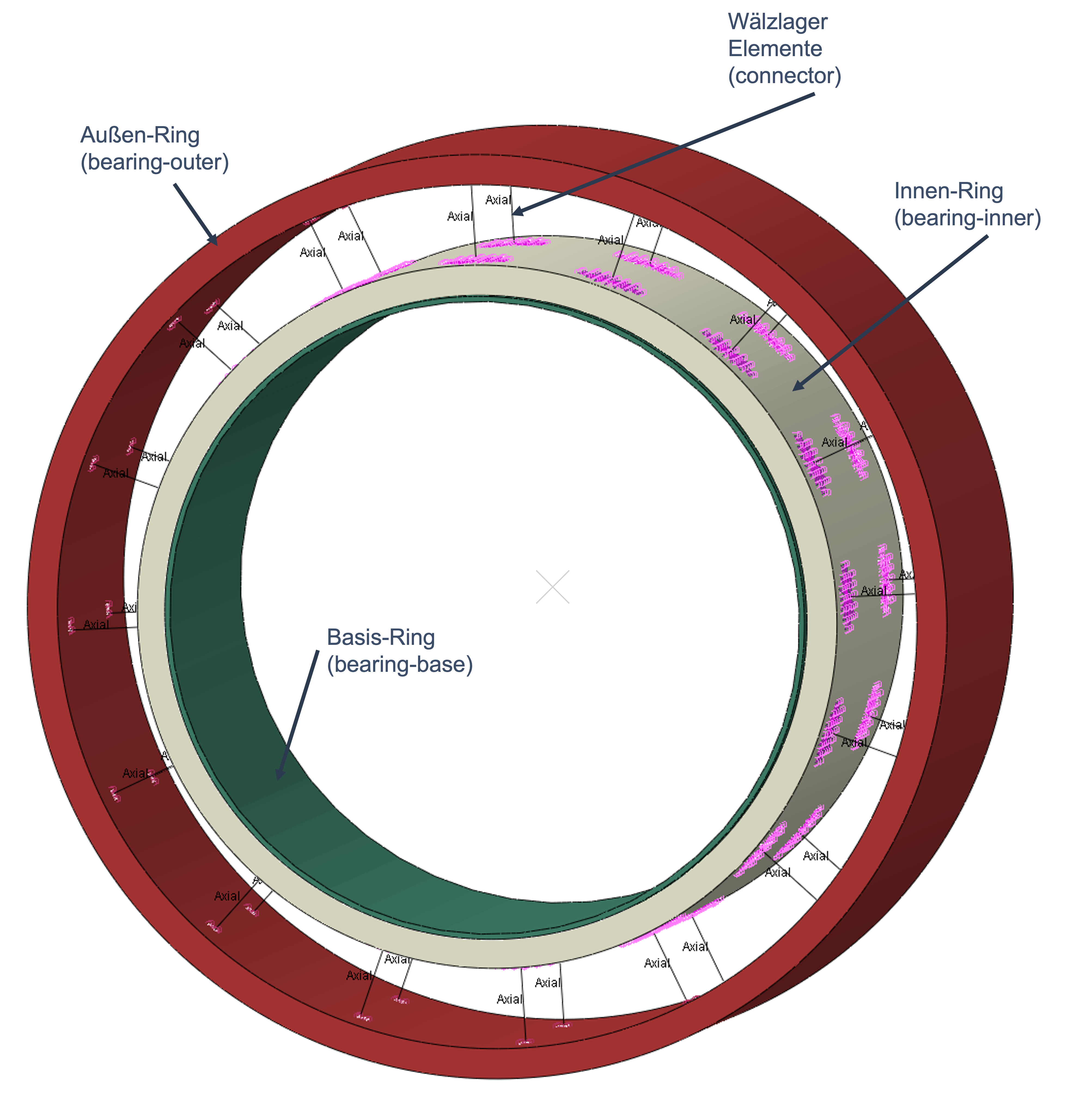
Bei der Berechnung von Welle-Nabe-Verbindungen wird das Lager meist vereinfacht durch die Kopplung eines Teils der Welle im Lagerbereich mit einem Zentral-Knoten abgebildet. Die Art der Kopplung und die richtige Wahl der Randbedingungen sind dann mögliche Fehlerquellen mit erheblichen Auswirkungen auf das Ergebnis. In einem ersten Ansatz wurde ein anderes Modell für die Lagerabbildung erstellt, siehe folgendes Bild. Ein solches Modell verändert aber das Konvergenzverhalten und führt zu einer Verlängerung der Berechnung.

Beschrieben wurden in einem früheren Beitrag die Vorteile einer Demokratisierung der Simulation. Um diese Vorteile nutzen zu können, bedarf es gemeinsamer Anstrengungen von Konstrukteuren und Berechnungs-Ingenieuren.

Die Güte und Prognosefähigkeit einer Simulation hängen von der Qualität der Abbildung von Geometrie, Material, Verbindungstechnik und den Algorithmen der Finite Element Methode ab. Es wurde aufgezeigt, daß selbst für eine vermeintlich einfache Problemstellung wie einer Welle-Nabe-Verbindung Voruntersuchungen für die Definition notwendiger Simulations-Parameter notwendig sind. Auch wurde aufgezeigt, daß Fehlerquellen einer vereinfachten Betrachtung aufgezeigt und gegebenenfalls durch Modelländerungen vermieden werden müssen.

Sicher gilt:

• Die Simulation muss einen Mehrwert im Produkt-Entstehungs-Prozess bieten.
• Die Simulation sollte prognosefähig sein.